Topological Sorting
Fundamentals
Topological sorting: In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
Kahn’s Algorithm
Directed Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// Kahn's algorithm
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new List[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new ArrayList<>();
}
int[] indegrees = new int[numCourses];
for (int[] p : prerequisites) {
graph[p[1]].add(p[0]);
indegrees[p[0]]++;
}
// zero indegree
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegrees[i] == 0) {
q.offer(i);
}
}
int[] order = new int[numCourses];
int count = 0;
while (!q.isEmpty()) {
int course = q.poll();
for (int neighbor : graph[course]) {
if (--indegrees[neighbor] == 0) {
q.offer(neighbor);
}
}
order[count++] = course;
}
return count == numCourses ? order : new int[0];
}
Find All Possible Recipes from Given Supplies
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {
int n = recipes.length;
// {ingredient : recipe index}
Map<String, List<Integer>> graph = new HashMap<>();
int[] indegree = new int[n];
Set<String> set = Arrays.stream(supplies).collect(Collectors.toSet());
for (int i = 0; i < n; i++) {
// if an ingredient is not in supplies, makes it a graph node
// i.e. supplied ingredients are omitted in the graph
for (String in : ingredients.get(i)) {
if (!set.contains(in)) {
graph.computeIfAbsent(in, k -> new ArrayList<>()).add(i);
// indegrees[i] denotes the number of unsupplied ingredients of the i-th recipe
indegrees[i]++;
}
}
}
// leaves are recipes with 0 indegree
// i.e. whose ingredients are all supplied
Queue<String> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (indegrees[i] == 0) {
q.offer(recipes[i]);
}
}
List<String> list = new ArrayList<>();
while (!q.isEmpty()) {
String node = q.poll();
if (graph.containsKey(node)) {
for (int i : graph.get(node)) {
if (--indegrees[i] == 0) {
q.offer(recipes[i]);
}
}
}
list.add(node);
}
return list;
}
Undirected Graph
For undirected graphs, leaves are nodes with degrees == 1.
Distance to a Cycle in Undirected Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public int[] distanceToCycle(int n, int[][] edges) {
int[] degrees = new int[n];
List<Integer>[] graph = new List[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] e : edges) {
graph[e[0]].add(e[1]);
graph[e[1]].add(e[0]);
degrees[e[0]]++;
degrees[e[1]]++;
}
// Enqueues leaves
Queue<Integer> q = new LinkedList<>();
// flags means "visited"
boolean[] flags = new boolean[n];
for (int i = 0; i < n; i++) {
// Undirected graph leaf
if (degrees[i] == 1) {
q.offer(i);
flags[i] = true;
}
}
while (!q.isEmpty()) {
int node = q.poll();
for (int neighbor : graph[node]) {
if (flags[neighbor]) {
continue;
}
// Undirected graph
if (--degrees[neighbor] == 1) {
q.offer(neighbor);
flags[neighbor] = true;
}
}
}
// DFS from the cycle to outer
// Now flags means "unvisited"
q.clear();
for (int i = 0; i < n; i++) {
if (!flags[i]) {
q.offer(i);
}
}
int[] answer = new int[n];
int level = 1;
while (!q.isEmpty()) {
for (int i = q.size(); i > 0; i--) {
int node = q.poll();
for (int neighbor : graph[node]) {
if (!flags[neighbor]) {
q.offer(neighbor);
answer[neighbor] = level;
flags[neighbor] = true;
}
}
}
level++;
}
return answer;
}
Path Length
Longest path in a DAG can be solved by topological sorting.
Longest Increasing Path in a Matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// pads the grid with zero as boundaries
int[][] matrix = new int[m + 2][n + 2];
for (int i = 0; i < m; i++) {
System.arraycopy(grid[i], 0, matrix[i + 1], 1, n);
}
int[][] outdegree = new int[m + 2][n + 2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int[] d: dir) {
if (matrix[i][j] < matrix[i + d[0]][j + d[1]]) {
outdegree[i][j]++;
}
}
}
}
Another solution is DFS + memoization
Number of Orderings
Number of topological orderings of a directed tree:
Count Ways to Build Rooms in an Ant Colony
\[\frac{n!}{\prod{s_i}}\]where \(s_i\) is the size of the subtree at the i-th node.
DAG
A topological ordering is possible iff the graph has no directed cycles, that is, iff it is a directed acyclic graph (DAG).
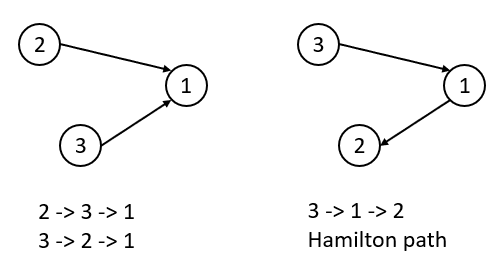
Uniqueness
If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian path in the DAG.
A Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once.
Iff a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path.
If a topological sort does not form a Hamiltonian path, it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public boolean sequenceReconstruction(int[] nums, List<List<Integer>> sequences) {
int n = nums.length;
// index[i]: index of element nums[i] in nums
int[] index = new int[n + 1];
for (int i = 0; i < n; i++) {
index[nums[i]] = i;
}
// pairs[i]: nums[i] and nums[i + 1] make a pair
boolean[] pairs = new boolean[n];
for (List<Integer> seq : sequences) {
for (int i = 0; i < seq.size(); i++) {
if (seq.get(i) > n) {
return false;
}
// each seq in sequences should be a subsequence of nums
if (i > 0 && index[seq.get(i - 1)] >= index[seq.get(i)]) {
return false;
}
// all pairs of consecutive elements in nums should be in some seq in sequences
if (i > 0 && index[seq.get(i - 1)] + 1 == index[seq.get(i)]) {
pairs[index[seq.get(i - 1)]] = true;
}
}
}
for (int i = 0; i < n - 1; i++) {
if (!pairs[i]) {
return false;
}
}
return true;
}
A more intuitive solution is to reconstruct the topological sort from sequences and check if it’s unique and equal to nums.
Two-level Topological Sort
Sort Items by Groups Respecting Dependencies
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
private List<Integer>[] groupGraph, itemGraph;
private int[] groupsIndegree, itemsIndegree;
public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
// maps items with -1 group to new isolated groups
// and updates the group count
for (int i = 0; i < n; i++) {
if (group[i] < 0) {
group[i] = m++;
}
}
this.itemGraph = new ArrayList[n];
this.groupGraph = new ArrayList[m];
for (int i = 0; i < n; i++) {
itemGraph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
groupGraph[i] = new ArrayList<>();
}
this.itemsIndegree = new int[n];
this.groupsIndegree = new int[m];
// builds items
for (int i = 0; i < n; i++) {
for (int item : beforeItems.get(i)) {
itemGraph[item].add(i);
itemsIndegrees[i]++;
}
}
// builds group
// multiple edges are possible
for (int i = 0; i < group.length; i++) {
int toGroup = group[i];
for (int fromItem : beforeItems.get(i)) {
int fromGroup = group[fromItem];
if (fromGroup != toGroup) {
groupGraph[fromGroup].add(toGroup);
groupsIndegrees[toGroup]++;
}
}
}
// topological sort
List<Integer> itemsList = sort(itemGraph, itemsIndegree, n);
List<Integer> groupsList = sort(groupGraph, groupsIndegree, m);
// detects if there are any cycles
if (groupsList.isEmpty() || itemsList.isEmpty()) {
return new int[0];
}
// maps items to their group in order
List<Integer>[] membersInGroup = new ArrayList[m];
for (int i = 0; i < m; i++) {
membersInGroup[i] = new ArrayList<>();
}
for (int item : itemsList) {
membersInGroup[group[item]].add(item);
}
int[] result = new int[n];
int index = 0;
for (int g : groupsList) {
for (int item : membersInGroup[g]) {
result[index++] = item;
}
}
return result;
}
private List<Integer> sort(List<Integer>[] graph, int[] indegree, int count) {
List <Integer> list = new ArrayList<>();
Queue <Integer> q = new LinkedList<>();
for (int i = 0; i < graph.length; i++) {
if (indegrees[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int node = q.poll();
count--;
list.add(node);
for (int neighbor : graph[node]) {
if (--indegrees[neighbor] == 0) {
q.offer(neighbor);
}
}
}
return count == 0 ? list : Collections.EMPTY_LIST;
}
Another solution is by DFS:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
private List<Integer>[] graph;
private int[] indegree;
private int n;
public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
this.n = n;
// items that belong to the same group are virtually bundled together
// n <= group node index <= n + m
//
// if k < n
// if k is in a group
// - graph[k] is inner-group after-items of item k
// - indegrees[k] is inner-group indegree of item k
// else if k is not in any group
// - graph[k] is after-items of item k
// - indegrees[k] is indegree of item k
// otherwise
// - graph[k] is members of group (k - n)
// - indegrees[k] is indegree of group (k - n)
this.graph = new ArrayList[n + m];
this.indegree = new int[n + m];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < n; i++) {
// bundles nodes that belong to the same group
// the new index becomes: n + group[i]
if (group[i] >= 0) {
graph[n + group[i]].add(i);
// marks indegree as 1
// so when we scan to find the 0-indegree node
// if index < n, it guarantees to be a node that doesn't belong to a group
indegrees[i]++;
}
}
for (int i = 0; i < n; i++) {
int ig = map(group, i);
for (int b : beforeItems.get(i)) {
int bg = map(group, b);
// current item and its before item are in the same group
if (bg == ig) {
graph[b].add(i);
// remember, inner-group indegrees start from 1
indegrees[i]++;
} else {
// either i is not in a group
// or i and b are in different groups
// this is for "external" links
graph[bg].add(ig);
indegrees[ig]++;
}
}
}
List<Integer> list = new ArrayList<>();
for (int i = 0; i < indegree.length; i++) {
// when indegrees[i] == 0
// if i < n, the node i doesn't belong to any group (see comments above)
// if i >= n, the dfs topologically sorts the members in the group
if (indegrees[i] == 0) {
dfs(i, list);
}
}
return list.size() == n ? list.stream().mapToInt(i -> i).toArray() : new int[0];
}
// maps the item to its group node index if it belongs to a group
// otherwise returns its item index
private int map(int[] group, int item) {
return group[item] < 0 ? item : group.length + group[item];
}
private void dfs(int curr, List<Integer> list) {
if (curr < n) {
list.add(curr);
}
// marks it as visited (-1)
// so the start condition of the dfs indegrees[node] == 0 won't be met again
indegrees[curr]--;
// if curr < n, and
// - curr doesn't belong to any group, then graph[curr] is its after-items
// - curr belongs to a group, then group[curr] is the after-items of the same groups
// otherwise, graph[curr] are the members of the group, and only members with degree 1 will be picked
for (int child : graph[curr]) {
// remember, inner-group indegrees are based on 1
if (--indegrees[child] == 0) {
dfs(child, list);
}
}
}
Centroids
Any connected graph without simple cycles is a tree. The number of centroids of a tree is no more than 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1) {
return Collections.singletonList(0);
}
List<Set<Integer>> tree = new ArrayList<>();
for (int i = 0; i < n; i++) {
tree.add(new HashSet<>());
}
for (int[] e : edges) {
tree.get(e[0]).add(e[1]);
tree.get(e[1]).add(e[0]);
}
// finds the leaves
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (tree.get(i).size() == 1) {
q.offer(i);
}
}
// trims the leaves until centroids
while (n > 2) {
n -= q.size();
for (int i = q.size(); i > 0; i--) {
int leaf = q.poll();
int neighbor = tree.get(leaf).iterator().next();
tree.get(neighbor).remove(leaf);
// undirected graph leaf
if (tree.get(neighbor).size() == 1) {
q.offer(neighbor);
}
}
}
return new ArrayList<>(q);
}
Diameter
diameter = 2 * level + number of centroids - 1
Count Subtrees With Max Distance Between Cities
+ Other Algorithms
+ DP
dp[node] denotes a certain state of all paths to this node.
Shortest Path
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int minimumTime(int n, int[][] relations, int[] time) {
List<Integer>[] graph = new List[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
int[] indegree = new int[n + 1];
for (int[] r : relations) {
graph[r[0]].add(r[1]);
indegrees[r[1]]++;
}
// DP: minimum time to reach this node
int[] cost = new int[n + 1];
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= n; i++) {
if (indegrees[i] == 0) {
q.offer(i);
cost[i] = time[i - 1];
}
}
while (!q.isEmpty()) {
int node = q.poll();
for (int neighbor : graph[node]) {
cost[neighbor] = Math.max(cost[neighbor], cost[node] + time[neighbor - 1]);
if (--indegrees[neighbor] == 0) {
q.offer(neighbor);
}
}
}
return Arrays.stream(cost).max().getAsInt();
}
Highest Frequency
Largest Color Value in a Directed Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public int largestPathValue(String colors, int[][] edges) {
int n = colors.length();
List<Integer>[] graph = new List[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
int[] indegree = new int[n];
for (int[] e : edges) {
graph[e[0]].add(e[1]);
indegrees[e[1]]++;
}
// dp[i][j]: max count of i-th node, j-th color
int[][] dp = new int[n][26];
// zero indegree
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (indegrees[i] == 0) {
q.offer(i);
dp[i][colors.charAt(i) - 'a'] = 1;
}
}
int count = 0, max = 0;
while (!q.isEmpty()) {
int node = q.poll();
count++;
// if max is updated at this node
// then the color of this node must be the most frequent
max = Math.max(max, dp[node][colors.charAt(node) - 'a']);
for (int child : graph[node]) {
// updates dp of child node
for (int i = 0; i < 26; i++) {
dp[child][i] = Math.max(dp[child][i], dp[node][i] + (colors.charAt(child) - 'a' == i ? 1 : 0));
}
if (--indegrees[child] == 0) {
q.offer(child);
}
}
}
return count == n ? max : -1;
}