Subtree
Binary Lifting
This is a good tutorial on Binary Lifting.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// dp[i][j] = j-th node's (2 ^ i)-th ancestor in the path
private int[][] dp;
private int maxPow;
// Binary lifting
public TreeAncestor(int n, int[] parent) {
// log_base_2(n)
this.maxPow = (int)(Math.log(n) / Math.log(2)) + 1;
this.dp = new int[maxPow][n];
// dp[0][j] = parent[j]: first parent (2^0) of each node is given
dp[0] = parent;
for (int i = 1; i < maxPow; i++) {
for (int j = 0; j < n; j++) {
// To find the (2 ^ i)-th ancestor of j,
// recursively finds j-th node's 2 ^ (i - 1)th ancestor's 2 ^ (i - 1)th ancestor
// 2 ^ i = 2 ^ (i - 1) + 2 ^ (i - 1)
int prev = dp[i - 1][j];
dp[i][j] = prev == -1 ? -1 : dp[i - 1][prev];
}
}
}
public int getKthAncestor(int node, int k) {
int currPow = maxPow;
while (k > 0 && node >= 0) {
if (k >= 1 << currPow) {
node = dp[currPow][node];
k -= 1 << currPow;
} else {
// takes smaller stride
currPow--;
}
}
return node;
}
Maximize Value of Function in a Ball Passing Game
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
long long getMaxFunctionValue(vector<int>& receiver, long long k) {
int m = 8 * sizeof(k) - __builtin_clzll(k), n = receiver.size();
// dp[i][j]: {id, value sum}
vector<vector<pair<int, long long>>> dp(m, vector<pair<int, long long>>(n));
for (int j = 0; j < n; j++) {
dp[0][j] = {receiver[j], receiver[j]};
}
for (int i = 0; i < m - 1; i++) {
for (int j = 0; j < n; j++) {
int r = dp[i][j].first;
dp[i + 1][j] = {dp[i][r].first, dp[i][j].second + dp[i][r].second};
}
}
// The binary form of k can be interpreted as sum of receivers of `curr`.
// `bit` is the most significant bit
function<long long(int, int)> f = [&](int curr, int bit) -> long long {
if (bit < 0) {
return 0;
}
if ((k & (1ll << bit)) == 0) {
return f(curr, bit - 1);
}
return dp[bit][curr].second + f(dp[bit][curr].first, bit - 1);
};
long long res = 0;
for (int i = 0; i < n; i++) {
res = max(res, f(i, m - 1) + i);
}
return res;
}
Lowest Common Ancestor
Tree recursion:
Lowest Common Ancestor of a Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private TreeNode lca = null;
// Relax the condition so the problem can be solved recursively:
// - if only p (or q) exists, returns p (or q)
// - if neither p or q exists, returns null
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// LCA is found, returns early
if (lca != null) {
return null;
}
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q), right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
lca = root;
return lca;
}
return left == null ? right : left;
}
Lowest Common Ancestor of a Binary Tree II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
private int count = 0;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode lca = dfs(root, p, q);
return count == 2 ? lca : null;
}
/**
* If subtree contains either p or q, returns this node;
* if subtree contains both p and q, returns LCA of them;
* otherwise, returns null.
*/
private TreeNode dfs(TreeNode node, TreeNode p, TreeNode q) {
if (node == null) {
return null;
}
TreeNode left = dfs(node.left, p, q), right = dfs(node.right, p, q);
if (node == p || node == q) {
count++;
return node;
}
if (left != null && right != null) {
return node;
}
return left == null ? right : left;
}
Lowest Common Ancestor of a Binary Tree III
1
2
3
4
5
6
7
8
public Node lowestCommonAncestor(Node p, Node q) {
Node a = p, b = q;
while (a != b) {
a = a == null ? q : a.parent;
b = b == null ? p : b.parent;
}
return a;
}
This solution stems from Intersection of Two Linked Lists.
The following LCA problem is solved by binary lifting. It also shows LCA can be used to compute variables between two tree nodes.
Minimum Edge Weight Equilibrium Queries in a Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
vector<vector<pair<int, int>>> g(n);
for (auto const& e : edges) {
g[e[0]].push_back(pair{e[1], e[2]});
g[e[1]].push_back(pair{e[0], e[2]});
}
// freqs[i][j]: freq of edges with weight j from root to node i
vector<vector<int>> freqs(n);
// d[i]: depth of node i
vector<int> depths(n, 0);
// Binary lifting
const int m = (int)log2(n) + 1;
vector<vector<int>> ancestors(m, vector<int>(n));
function<void(int, int, int)> dfs = [&](int node, int parent, int d) -> void
{
ancestors[0][node] = parent;
depths[node] = d;
for (auto const& [child, weight] : g[node])
{
if (child != parent)
{
freqs[child] = freqs[node];
freqs[child][weight]++;
dfs(child, node, d + 1);
}
}
};
freqs[0] = vector<int>(27, 0);
dfs(0, 0, 0);
for (int i = 1; i < m; i++)
{
for (int j = 0; j < n; j++)
{
ancestors[i][j] = ancestors[i - 1][ancestors[i - 1][j]];
}
}
auto lca = [&](int x, int y) -> int
{
if (depths[x] > depths[y])
{
swap(x, y);
}
// Move y to the same depth as x
for (int p = 0; (1 << p) <= depths[y] - depths[x]; p++)
{
if ((1 << p) & (depths[y] - depths[x]))
{
y = ancestors[p][y];
}
}
for (int p = m - 1; p >= 0; p--)
{
if (ancestors[p][x] != ancestors[p][y])
{
x = ancestors[p][x];
y = ancestors[p][y];
}
}
return x == y ? x : ancestors[0][x];
};
vector<int> answer;
for (auto const& q: queries)
{
int x = q[0], y = q[1], a = lca(x, y);
// Total weights between x and y
int len = depths[x] + depths[y] - 2 * depths[a];
// Max freq of weights between x and y
int max_f = 0;
for (int w = 1; w < freqs[0].size(); w++)
{
max_f = max(max_f, freqs[x][w] + freqs[y][w] - freqs[a][w] * 2);
}
answer.push_back(len - max_f);
}
return answer;
}
Cycle Length Queries in a Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int[] cycleLengthQueries(int n, int[][] queries) {
int m = queries.length;
int[] answer = new int[m];
for (int i = 0; i < m; i++) {
answer[i]++;
// finds lca
int a = queries[i][0], b = queries[i][1];
while (a != b) {
if (a > b) {
a /= 2;
} else {
b /= 2;
}
answer[i]++;
}
}
return answer;
}
Find Distance in a Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
private int d = -1;
public int findDistance(TreeNode root, int p, int q) {
dfs(root, p, q);
return Math.max(d, 0);
}
private int dfs(TreeNode node, int p, int q) {
if (node == null) {
return -1;
}
int left = dfs(node.left, p, q), right = dfs(node.right, p, q);
if (node.val == p || node.val == q) {
if (left < 0 && right < 0) {
return 0;
}
d = Math.max(left, right) + 1;
return -1;
}
if (left >= 0 && right >= 0) {
d = left + right + 2;
return -1;
}
if (left >= 0 || right >= 0) {
return Math.max(left, right) + 1;
}
return -1;
}
Lowest Common Ancestor of Deepest Leaves
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public TreeNode lcaDeepestLeaves(TreeNode root) {
return dfs(root).getValue();
}
// <depth, lowest_common_ancestor>
private Pair<Integer, TreeNode> dfs(TreeNode node) {
if (node == null) {
return new Pair(0, null);
}
Pair<Integer, TreeNode> l = dfs(node.left), r = dfs(node.right);
int d1 = l.getKey(), d2 = r.getKey();
return new Pair(Math.max(d1, d2) + 1, d1 == d2 ? node : d1 > d2 ? l.getValue() : r.getValue());
}
Step-By-Step Directions From a Binary Tree Node to Another
The shortest path between any two nodes in a tree must pass through their Lowest LCA. Find the two paths root -> startValue and root -> destValue, then remove the longest common prefix from the two path strings.
Rerooting
Count Number of Possible Root Nodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
private List<Integer>[] tree;
// if guesses contains [u, v], guessGraph[u] contains v
private Set<Integer>[] guessGraph;
// dp map while re-rooting
// map[d]: number of nodes whose number of correct guesses is c0 + d, if the node is viewed as root
private Map<Integer, Integer> map = new HashMap<>();
// correct guesses when the root is at node 0
private int c0 = 0;
public int rootCount(int[][] edges, int[][] guesses, int k) {
int n = edges.length + 1;
this.tree = new List[n];
this.guessGraph = new Set[n];
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
guessGraph[i] = new HashSet<>();
}
for (int[] e : edges) {
tree[e[0]].add(e[1]);
tree[e[1]].add(e[0]);
}
for (int[] g : guesses) {
guessGraph[g[0]].add(g[1]);
}
dfs(0, -1, 0);
int sum = 0;
for (var e : map.entrySet()) {
sum += e.getValue() * (c0 + e.getKey() >= k ? 1 : 0);
}
return sum;
}
// re-rooting
// @param delta if the number of correct guesses is c when node is the root, then delta = c - c0
private void dfs(int node, int parent, int delta) {
map.put(delta, map.getOrDefault(delta, 0) + 1);
for (int child : tree[node]) {
if (child != parent) {
c0 += guessGraph[node].contains(child) ? 1 : 0;
// when root changes from node to child
// the number of correct guesses changes by one at most
// i.e. guess [node, child] changes from true to false,
// while guess [child, node] changes from false to true
dfs(child, node, delta + (guessGraph[child].contains(node) ? 1 : 0) - (guessGraph[node].contains(child) ? 1 : 0));
}
}
}
Difference Between Maximum and Minimum Price Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// maxPaths[i]: when the tree is rooted at node 0, max path sum of subtree of root node i
private long[] maxPaths;
private long maxCost;
public long maxOutput(int n, int[][] edges, int[] price) {
List<Integer>[] tree = new List[n];
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
for (int[] e : edges) {
tree[e[0]].add(e[1]);
tree[e[1]].add(e[0]);
}
this.maxPaths = new long[n];
// first, roots the tree at node 0
dfs(tree, 0, -1, price);
// then, use each node as tree root and computes the result
reroot(tree, 0, -1, price, 0);
// min price sum is always the node itself
// so for a particular node as root, its cost is the max of its child paths (excluding itself)
return maxCost;
}
private long dfs(List<Integer>[] tree, int node, int parent, int[] price) {
long max = 0;
for (int child: tree[node]) {
if (child != parent) {
max = Math.max(max, dfs(tree, child, node, price));
}
}
return maxPaths[node] = price[node] + max;
}
private void reroot(List<Integer>[] tree, int node, int parent, int[] price, long maxParentPath) {
int maxChild = -1;
// finds max two path sums among all children of `node`, when the tree root is at 0
long max1 = 0, max2 = 0;
for (int child : tree[node]) {
if (child != parent) {
if (maxPaths[child] > max1) {
max2 = max1;
max1 = maxPaths[child];
maxChild = child;
} else if (maxPaths[child] > max2) {
max2 = maxPaths[child];
}
}
}
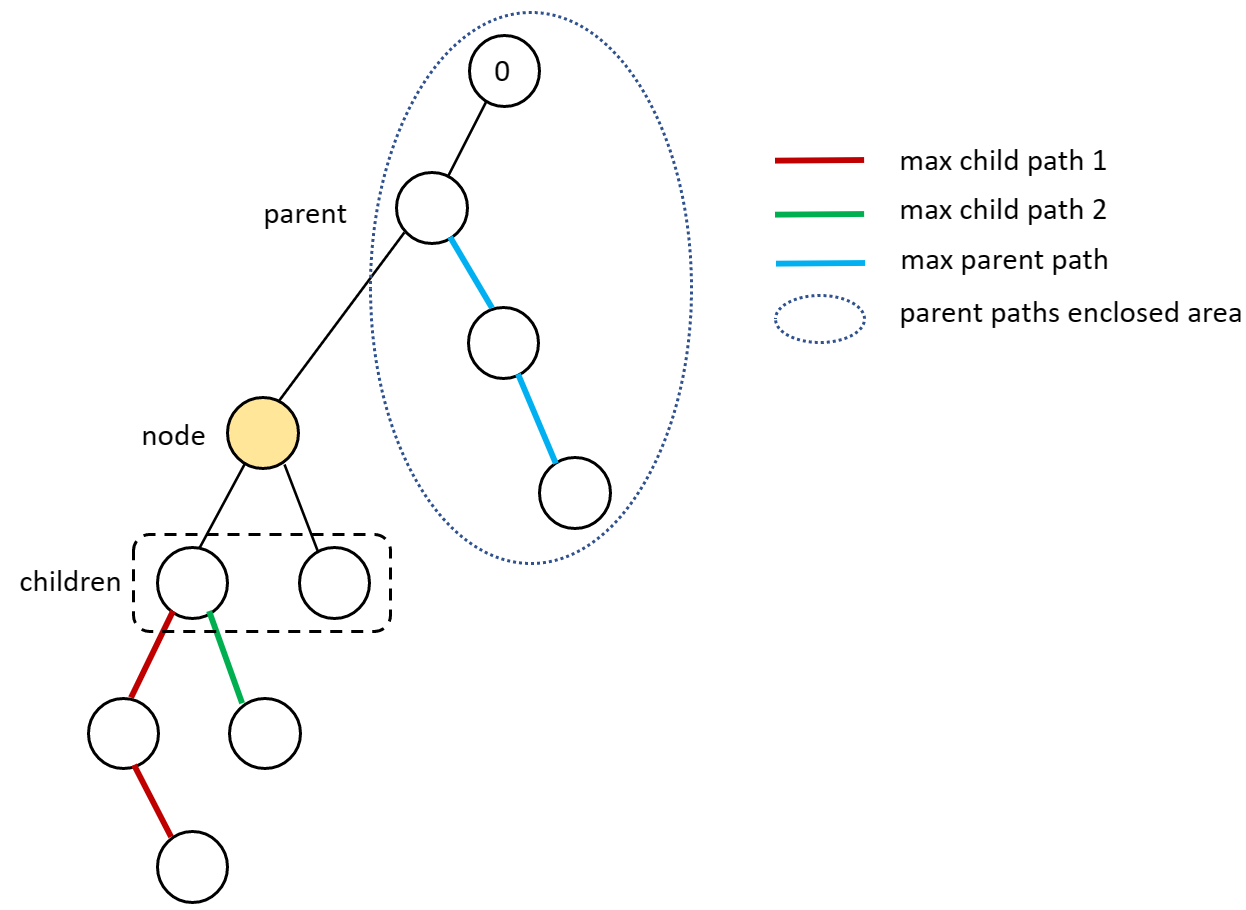
// maxParentPath is the max of the paths of `parent` that `node` is not on
maxCost = Math.max(maxCost, Math.max(max1, maxParentPath));
for (int child: tree[node]) {
if (child != parent) {
// when `node` becomes parent, the new `maxParentPath` is the max of:
// 1. max child path that `child` is not on
// - if `child` is not on `node`'s max path, it's `node`'s max path (max1)
// - otherwise, it's `child` path's max sibling (max2)
// 2. `node`'s maxParentPath
reroot(tree, child, node, price, price[node] + Math.max(maxChild == child ? max2 : max1, maxParentPath));
}
}
}
Rerooting is a general algorithm that can be used in many cases. However, a smarter approach is to use a one-pass DFS.
Non-overlapping Subtrees
Maximum XOR of Two Non-Overlapping Subtrees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
private List<Integer>[] tree;
private long[] sums;
private TrieNode root;
private long max = 0;
private int[] values;
public long maxXor(int n, int[][] edges, int[] values) {
this.tree = new List[n];
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
for (int[] e : edges) {
tree[e[0]].add(e[1]);
tree[e[1]].add(e[0]);
}
this.sums = new long[n];
this.values = values;
dfs(0, -1);
this.root = new TrieNode();
for (int child : tree[0]) {
dfs2(child, 0);
}
return max;
}
private long dfs(int node, int parent) {
sums[node] += values[node];
for (int child : tree[node]) {
if (child != parent) {
sums[node] += dfs(child, node);
}
}
return sums[node];
}
// 421. Maximum XOR of Two Numbers in an Array
private void dfs2(int node, int parent) {
TrieNode curr = root;
long xor = 0;
for (int i = 63; i >= 0; i--) {
int b = (int)((sums[node] >> i) & 1);
if (curr.children[b ^ 1] != null) {
curr = curr.children[b ^ 1];
xor = (xor << 1) + 1;
} else if (curr.children[b] != null) {
curr = curr.children[b];
xor <<= 1;
} else {
break;
}
}
max = Math.max(max, xor);
for (int child : tree[node]) {
if (child != parent) {
dfs2(child, node);
}
}
// adds sums[node] at last (postorder) to make sure the subtrees are non-overlapping
curr = root;
for (int i = 63; i >= 0; i--) {
int b = (int)((sums[node] >> i) & 1);
if (curr.children[b] == null) {
curr.children[b] = new TrieNode();
}
curr = curr.children[b];
}
}
class TrieNode {
TrieNode[] children = new TrieNode[2];
}