Stack

Java implementations of Stack:

• Deque (Stack)
• StringBuilder
• Array

Binary Searchable Numbers in an Unsorted Array

public int binarySearchableNumbers(int[] nums) {
    int n = nums.length;
    // for an element to be found,
    // it should be greater that all elements before it,
    // and smaller than all element after it
    Deque<Integer> st = new ArrayDeque<>();
    int max = Integer.MIN_VALUE;
    for (int num : nums) {
        // monotonically increasing
        // pops stack element if it's greater than num
        // ensures in-stack elements always < later elements
        while (!st.isEmpty() && num < st.peek()) {
            st.pop();
        }

        // num > all previous elements
        if (num > max) {
            st.push(num);
            max = num;
        }
    }
    return st.size();
}

Create Maximum Number

public int[] maxNumber(int[] nums1, int[] nums2, int k) {
    int n1 = nums1.length, n2 = nums2.length;
    int[] result = new int[k];
    // picks i digits from nums1
    // picks (k - i) digits from nums2
    // 0 <= i <= k
    // 0 <= i <= n1
    // 0 <= k - i <= n2 => i >= k - n2
    for (int i = Math.max(0, k - n2); i <= Math.min(k, n1); i++) {
        int[] candidate = merge(maxArray(nums1, i), maxArray(nums2, k - i), k);
        if (isGreaterThanOrEqualTo(candidate, 0, result, 0)) {
            result = candidate;
        }
    }
    return result;
}

private int[] merge(int[] nums1, int[] nums2, int k) {
    int[] result = new int[k];
    int i = 0, j = 0, index = 0;
    while (index < k) {
        result[index++] = isGreaterThanOrEqualTo(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];
    }
    return result;
}

// Check if nums1[i:] >= nums2[j:]
private boolean isGreaterThanOrEqualTo(int[] nums1, int i, int[] nums2, int j) {
    int n1 = nums1.length, n2 = nums2.length;
    while (i < n1 && j < n2 && nums1[i] == nums2[j]) {
        i++;
        j++;
    }
    return j == n2 || (i < n1 && nums1[i] >= nums2[j]);
}

/**
 * Creates the maximum number of length k from digits of the array.
 * @param nums number represented as an array
 * @param k length of the result number
 * @return the maximum number represented as an array
 */
private int[] maxArray(int[] nums, int k) {
    int n = nums.length;
    Deque<Integer> st = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        // monotonically decreasing stack
        // st.size + n - i > k means if we push all the remaining digits to the stack
        // the stack size will be greater than k
        // so we need to pop the stack to make room
        while (st.size() + n - i > k && !st.isEmpty() && nums[i] > st.peek()) {
            st.pop();
        }
        if (st.size() < k) {
            st.push(nums[i]);
        }
    }

    int[] result = new int[k];
    for (int i = k - 1; i >= 0; i--) {
        result[i] = st.pop();
    }
    return result;
}

Use array as a stack:

private int[] maxArray(int[] nums, int k) {
    int n = nums.length;
    // this array is used as a stack, too
    int[] result = new int[k];
    for (int i = 0, j = 0; i < n; i++) {
        while (n - i + j > k && j > 0 && nums[i] > result[j - 1]) {
            j--;
        }

        if (j < k) {
            result[j++] = nums[i];
        }
    }
    return result;
}

Number of Valid Subarrays

public int validSubarrays(int[] nums) {
    int count = 0;
    Deque<Integer> st = new ArrayDeque<>();
    for (int num : nums) {
        while (!st.isEmpty() && num < st.peek()) {
            st.pop();
        }
        st.push(num);
        count += st.size();
    }
    return count;
}

Jump Game V

It’s easy to come up with an O(nd) top-down DP solution.

// O(n)
public int maxJumps(int[] arr, int d) {
    int n = arr.length;

    // dp[i]: max number of indices we can visit from index i
    int[] dp = new int[n];
    Arrays.fill(dp, 1);

    // stack1 is the main stack
    Deque<Integer> st1 = new ArrayDeque<>(), st2 = new ArrayDeque<>();
    for (int i = 0; i <= n; i++) {
        // stack1 is monotonically decreasing
        // starts popping stack1 when the next element is greater, or it's the end of the array
        while (!st1.isEmpty() && (i == n || arr[i] > arr[st1.peek()])) {
            // top of the stack
            int top = arr[st1.peek()];

            // pops all indices in the stack whose elements equal top
            while (!st1.isEmpty() && top == arr[st1.peek()]) {
                // i -> j is a valid jump
                int j = st1.pop();
                if (i < n && i - j <= d) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }

                // pushes the current index to the stack2
                st2.push(j);
            }

            // stack2 stores all the indices whose elements equal the previous stack1.top
            // pops and processes each
            while (!st2.isEmpty()) {
                int j = st2.pop();
                // current stack1.top -> previous top is a valid jump
                if (!st1.isEmpty() && j - st1.peek() <= d) {
                    dp[st1.peek()] = Math.max(dp[st1.peek()], dp[j] + 1);
                }
            }
        }
        st1.push(i);
    }

    return Arrays.stream(dp).max().getAsInt();
}

Car Fleet II

public double[] getCollisionTimes(int[][] cars) {
    int n = cars.length;
    // monotonically decreasing stack wrt the collision time
    Deque<Integer> st = new ArrayDeque<>();
    double[] answer = new double[n];

    // iterates backwards
    for (int i = n - 1; i >= 0; i--) {
        answer[i] = -1;
        // top car doesn't collide with the current car if:
        // 1. speed of i-th car is no greater than the top car, or
        // 2. top car has already collided with another car (e.g. j-th car),
        //    thus i-th car would possibly collide with j-th car instead, and we need to pop the top
        //    iow, if i-th car can't catch (i + 1)-th car, before (i + 1)-th car catches (i + 2)-th car,
        //    then we can think of (i + 2)-th car as the candidate, removing (i + 1)-th car
        while (!st.isEmpty()
               && (cars[i][1] <= cars[st.peek()][1]
               || (computeTime(cars, i, st.peek()) >= answer[st.peek()] && answer[st.peek()] > 0))) {
            st.pop();
        }

        if (!st.isEmpty()) {
            answer[i] = computeTime(cars, i, st.peek());
        }
        st.push(i);
    }
    return answer;
}

// computes the time car i takes to catch car j
// i is faster than j
private double computeTime(int[][] cars, int i, int j) {
    return (double)(cars[j][0] - cars[i][0]) / (cars[i][1] - cars[j][1]);
}

In the problem below, the monotonicity of the stack is not straightforward:

Maximum Number of Books You Can Take

public long maximumBooks(int[] books) {
    Deque<Integer> st = new ArrayDeque<>();
    // pushes a virtual index to makes formula simple
    st.push(-1);

    long max = 0, curr = 0;
    for (int i = 0; i < books.length; i++) {
        // monotonically increasing stack
        // pops a shelf j if the b[j] > b[i] - (i - j)
        // e.g. [3, 5, 4] -> [2, 3, 4]
        // b[1]: 5 > 4 - 1
        // b[0]: 3 > 4 - 2
        while (st.peek() >= 0 && books[i] < books[st.peek()] + i - st.peek()) {
            int top = st.pop();
            curr -= sum(books[top], top - st.peek());
        }

        // uses the current shelf i as the last element of an arithmetic sequence (d = 1)
        // the sequence stops by st.peek()
        curr += sum(books[i], i - st.peek());
        st.push(i);
        max = Math.max(max, curr);
    }
    return max;
}

// sum of {an - n + 1, an - n + 2, ..., an}
private long sum(long an, int n) {
    long a1 = Math.max(0, an - n + 1);
    return (a1 + an) * (an - a1 + 1) / 2;
}

Histogram

The problem Largest Rectangle in Histogram deserves a closer look. The stack approach can be applied to many similar problems, like rectangle count/max area in a matrix.

Maximal Rectangle

int maximalRectangle(vector<vector<char>>& matrix) {
    int m = matrix.size(), n = matrix[0].size(), area = 0;
    vector<int> heights(n);
    stack<int> st;
    for (int i = 0; i < m; i++) {
        stack<int>().swap(st);
        st.push(-1);

        for (int j = 0; j <= n; j++) {
            // Histogram height array in each row
            if (j < n) {
                heights[j] = matrix[i][j] == '0' ? 0 : heights[j] + 1;
            }

            // 84. Largest Rectangle in Histogram
            while (st.top() >= 0 && (j == n || heights[j] < heights[st.top()])) {
                int h = heights[st.top()];
                st.pop();
                int w = j - 1 - st.top();
                area = max(area, h * w);
            }
            st.push(j);
        }
    }
    return area;
}

Count Submatrices With All Ones

public int numSubmat(int[][] mat) {
    int m = mat.length, n = mat[0].length, count = 0;
    // sums[i]: count of all-one submatrices with i as the right side
    int[] sums = new int[n];
    int[] heights = new int[n];

    for (int i = 0; i < m; i++) {
        Deque<Integer> st = new ArrayDeque<>();
        st.push(-1);
        Arrays.fill(sums, 0);

        for (int j = 0; j < n; j++) {
            // histogram height array in each row
            heights[j] = mat[i][j] == 0 ? 0 : heights[j] + 1;

            // 84. Largest Rectangle in Histogram
            while (st.peek() >= 0 && heights[j] < heights[st.peek()]) {
                st.pop();
            }

            // counts the all-one matrices whose bottom is at current row
            // and right side is on heights[j]
            int prev = st.peek();
            sums[j] = (prev < 0 ? 0 : sums[prev]) + heights[j] * (j - prev);
            st.push(j);
        }

        count += Arrays.stream(sums).sum();
    }

    return count;
}

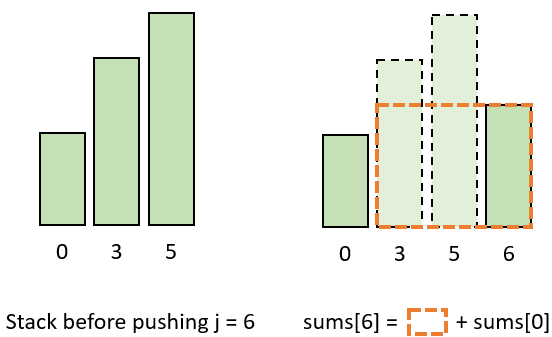
Instead of maining an extra array int[] sums, we can use {index, sum} as the compound stack element.

The final result is a culumative sum. The following solution gets rid of the extra array int[] sums and keeps using the single index stack element:

public int numSubmat(int[][] mat) {
    int m = mat.length, n = mat[0].length, count = 0;
    int[] heights = new int[n];

    for (int i = 0; i < m; i++) {
        Deque<Integer> st = new ArrayDeque<>();
        st.push(-1);

        // this is sums[j] in the above solution
        int sum = 0;
        for (int j = 0; j < n; j++) {
            // histogram height array in each row
            heights[j] = mat[i][j] == 0 ? 0 : heights[j] + 1;

            // subtracts sums[prev + 1], ..., sums[j - 1] in the above solution
            // that yields to sums[prev]
            while (st.peek() >= 0 && heights[j] < heights[st.peek()]) {
                int top = st.pop();
                sum -= heights[top] * (top - st.peek());
            }

            // rhs is the new count which has j as right side
            sum += heights[j] * (j - st.peek());
            count += sum;
            st.push(j);
        }
    }

    return count;
}

Lookahead

Use an auxiliary array to check the occurrences of certain elements in later inputs.

Remove Duplicate Letters

public String removeDuplicateLetters(String s) {
    // last index
    int[] last = new int[26];
    for (int i = 0; i < s.length(); i++) {
        last[s.charAt(i) - 'a'] = i;
    }

    // each character appears in the stack once and only once
    Deque<Integer> st = new ArrayDeque<>();
    boolean[] inStack = new boolean[26];
    for (int i = 0; i < s.length(); i++) {
        int c = s.charAt(i) - 'a';
        if (!inStack[c]) {
            // if c is less than stack top, and the top will appear later,
            // pops the top
            while (!st.isEmpty() && c < st.peek() && i < last[st.peek()]) {
                inStack[st.pop()] = false;
            }
            st.push(c);
            inStack[c] = true;
        }
    }

    StringBuilder sb = new StringBuilder();
    for (int i : st) {
        sb.append((char)('a' + i));
    }
    return sb.reverse().toString();
}

Using a Robot to Print the Lexicographically Smallest String

public String robotWithString(String s) {
    int[] count = new int[26];
    for (char ch : s.toCharArray()) {
        count[ch - 'a']++;
    }

    Deque<Character> st = new LinkedList<>();
    StringBuilder sb = new StringBuilder();
    int minCharIndex = 0;
    for (char ch : s.toCharArray()) {
        // always pushes the char to stack
        // then decides which operation to take next
        st.push(ch);
        count[ch - 'a']--;

        // finds the smallest unused char
        while (minCharIndex < count.length && count[minCharIndex] == 0) {
            minCharIndex++;
        }

        while (!st.isEmpty() && minCharIndex >= st.peek() - 'a') {
            sb.append(st.pop());
        }
    }
    return sb.toString();
}

Smallest K-Length Subsequence With Occurrences of a Letter

public String smallestSubsequence(String s, int k, char letter, int repetition) {
    // count of `letter`
    int count = (int)s.chars().filter(ch -> ch == letter).count();
    int n = s.length();

    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < n; i++) {
        char c = s.charAt(i);
        // if the current character can improve the lexicographical order, we pop the top if:
        // - there are enough remaining characters to construct a k-size string
        // - if the top is the same as letter, then the number of remaining letters >= `repetition`.
        //   number of remaining letter = count - 1 (-1 is the stack top)
        while (sb.length() > 0 && c < sb.charAt(sb.length() - 1) && n - i > k - sb.length()
               && (sb.charAt(sb.length() - 1) != letter || count > repetition)) {
            // pops
            char top = sb.charAt(sb.length() - 1);
            sb.deleteCharAt(sb.length() - 1);
            if (top == letter) {
                repetition++;
            }
        }

        if (sb.length() < k) {
            if (c == letter) {
                sb.append(c);
                repetition--;
            } else if (k - sb.length() > repetition) {
                // k - st.size() - repetition is the number of non-letter characters that need to be pushed
                sb.append(c);
            }
        }

        if (c == letter) {
            count--;
        }
    }
    return sb.toString();
}

Flatten Nested List Iterator

private Deque<NestedInteger> st;

public NestedIterator(List<NestedInteger> nestedList) {
    st = new ArrayDeque<>();
    pushToStack(nestedList);
}

@Override
public Integer next() {
    // caller doesn't necessarily calls hasNext() before next()
    return hasNext() ? st.pop().getInteger() : null;
}

@Override
public boolean hasNext() {
    while (!st.isEmpty()) {
        if (st.peek().isInteger()) {
            return true;
        }
        pushToStack(st.pop().getList());
    }
    return false;
}

private void pushToStack(List<NestedInteger> nestedList) {
    for (int i = nestedList.size() - 1; i >= 0; i--) {
        st.push(nestedList.get(i));
    }
}

Ternary Expression Parser

public String parseTernary(String expression) {
    Deque<Character> st = new ArrayDeque<>();
    char op = ' ';
    for (int i = expression.length() - 1; i >= 0; i--) {
        char c = expression.charAt(i);
        if (c == '?' || c == ':') {
            op = c;
        } else {
            if (op == '?') {
                char c1 = st.pop(), c2 = st.pop();
                st.push(c == 'T' ? c1 : c2);
            } else {
                st.push(c);
            }
        }
    }
    return String.valueOf(st.peek());
}

Parsing

Basic Calculator

public int calculate(String s) {
    // stores operands and signs alternatively
    Deque<Integer> stack = new ArrayDeque<>();
    int result = 0;
    int operand = 0, sign = 1;

    for (char c : s.toCharArray()) {
        if (Character.isDigit(c)) {
            operand = 10 * operand + c - '0';
        } else if (c == '+' || c == '-') {
            result += sign * operand;
            sign = c == '+' ? 1 : -1;
            operand = 0;
        } else if (c == '(') {
            stack.push(result);
            stack.push(sign);
            sign = 1;
            result = 0;
        } else if (c == ')') {
            result += sign * operand;
            result *= stack.pop();  // sign
            result += stack.pop();  // operand
            operand = 0;
        }
    }

    // + sign * operand at '+', '-', ')' or end of s
    return result + sign * operand;
}