三国杀武将技能概率

Posted Jul 4, 2023 Updated Jan 2, 2026

By Qinghao Hou

86 min read

三国杀武将技能概率

前言

本文的主体内容取自于本人十年前在百度帖吧三国杀吧的一篇帖子：【理论】数学与三国杀——三国杀武将技能概率。现加以整理、改进和删增。

本文通过研究《三国杀》中部分武将技能所涉及的概率与期望，对这些技能的强度与收益进行定量刻画，从而为玩家在特定对局中的选将、技能发动时机及出牌顺序提供决策参考。

研究范围

卡牌

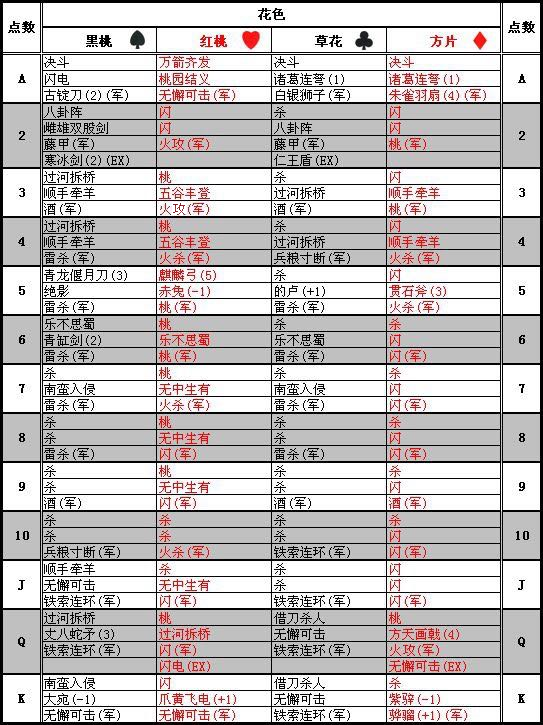
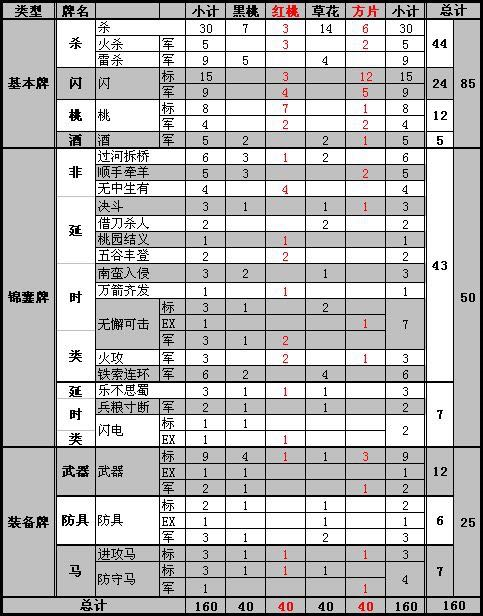
本文只考察军争篇卡牌。其点数、花色以及类型具体分布如下：

（图片来源：https://www.cnblogs.com/yhm138/articles/14091928.html，有勘误）

（图片来源：https://www.cnblogs.com/yhm138/articles/14091928.html）

数学模型

为便于统一讨论，本文将技能效果抽象为随机变量，并对其概率分布及数学期望进行分析。文中所称“期望”，均指技能触发结果或收益函数所对应随机变量的数学期望。

理想模型

若无特殊说明，本文所采用的数学模型均为理想模型，即假设任意一个时刻，牌堆中的卡牌数量无限多，且某牌按照其在上述军争篇中的概率均匀分布（并假设各次抽牌在概率意义上相互独立）。例如：

任一花色的概率为$1/4$
任一点数的概率为$1/13$¹
普通（非延时类）锦囊牌的概率为$43/160$

该假设并非对真实牌堆的物理描述，而是用于简化计算、刻画长期平均行为的数学近似。

无限牌堆模型实际上意味着有放回抽样。

在此基础上，关于拼点，我们进一步假设拼点双方亮出的牌的点数均匀分布。由对称性或直接计数易知，拼点赢的概率为$\frac{6}{13}$。

此外，本文中所有的小数结果仅保留四位有效数字。

现实模型

在某些情况下，本文也会采用现实模型。该模型有以下特点：

游戏模式为军争篇八人场
不放回抽样
假设在整局游戏过程中：
- 场上平均存活角色数为 4
- 每名角色平均拥有手牌 2 张、装备牌 2 张
- 场上平均存在 1 张判定牌。

这样，牌堆中的牌数平均为：$160-4*(2+2)-1=143$。

理想模型用于刻画技能的统计平均强度与内在概率结构，而现实模型则用于评估这些结论在标准军争局中的数值偏差。

武将

文中所涉及到的武将选取自以下系列：

标准版
神话再临·风火林山阴雷
一将成名2011-2015，2022-2024
原创之魂2016-2017
SP

另外，有些武将技能的概率计算过于简单直白，也不在本篇的讨论之列，如:

夏侯惇刚烈（成功概率$3/4$）
神关羽武魂（失败概率$13/160 = 0.08125$）
顾雍秉壹（摸牌概率$1/2^{X-1}$）
辛宪英（原创之魂2017）忠鉴（手牌上限减少概率$1/2*12/13 = 6/13 \approxeq 0.4615$）。
张星彩枪舞（参考下表【杀】的点数分布）

点数	A	2	3	4	5	6	7	8	9	10	J	Q	K
【杀】数量	0	1	1	4	4	4	6	7	5	8	3	0	1

秦宓天辩（拼点赢概率可拆解为若干互斥情形的加权和，其计算结果为$3/52*1/13\sum_{i=0}^{11}i+16/52 = 203/338 \approxeq 0.6006$）
夏侯楙（一将成名2023）统围（当其他角色下一次使用牌结算结束后，若认为此牌为随机选择，则此牌的点数不大于其中一张重铸牌且不小于另一张的概率为$\frac{\lvert X_1 - X_2 \rvert}{13}$，其中$X1,X2$为两张重铸牌的点数）

上述技能要么概率结构过于直接，要么计算不涉及复杂的条件依赖，因此不作为本文重点讨论对象。

武将技能概率

伯努利试验

本文采用负二项分布“在达到固定成功次数$r$前所经历的失败次数（或总试验次数）”的参数化方式。

有一些武将技能概率问题符合典型的伯努利试验下的概率分布。我们以邓艾、甄姬和孟获三名武将的技能为例一一说明。对每名武将都会采用理想模型（有放回）和现实模型（不放回）进行分析。

邓艾（神话再临·山）

屯田：每次当你于回合外失去牌时，可进行一次判定，将非♥结果的判定牌置于你的武将牌上，称为“田”；每有一张田，你计算与其他角色的距离便-1。

凿险：觉醒技，回合开始阶段，若田的数量达到3张或更多，你须减1点体力上限，并永久获得技能“急袭”（出牌阶段，你可以把任意一张田当【顺手牵羊】使用）。

下面我们来研究可以发动觉醒技凿险时所需的屯田次数。

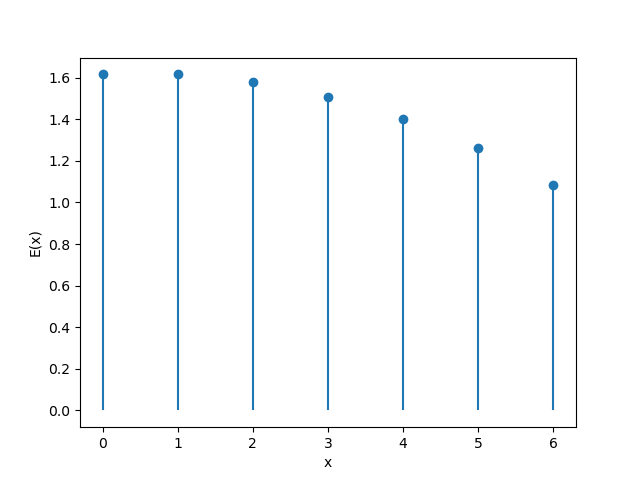
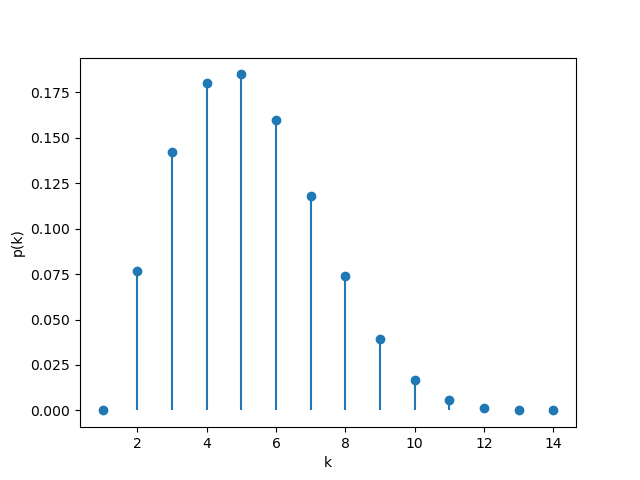
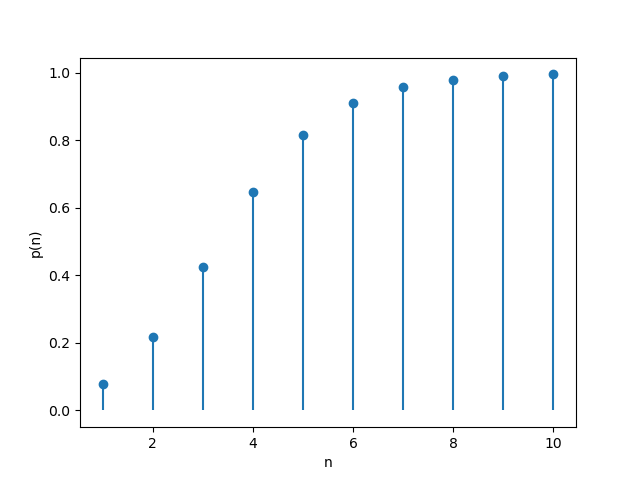
【理想模型】

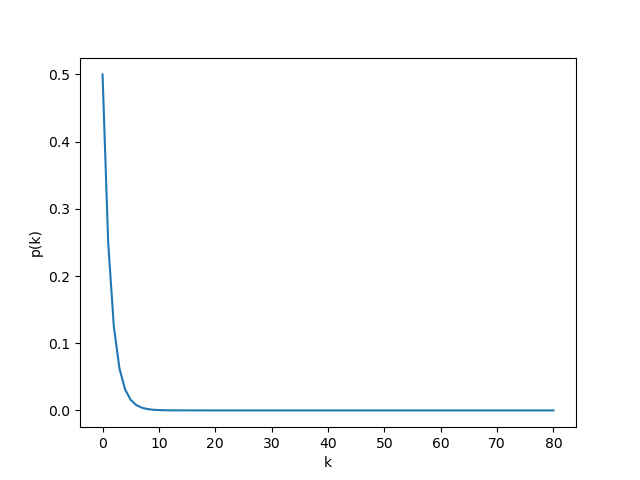
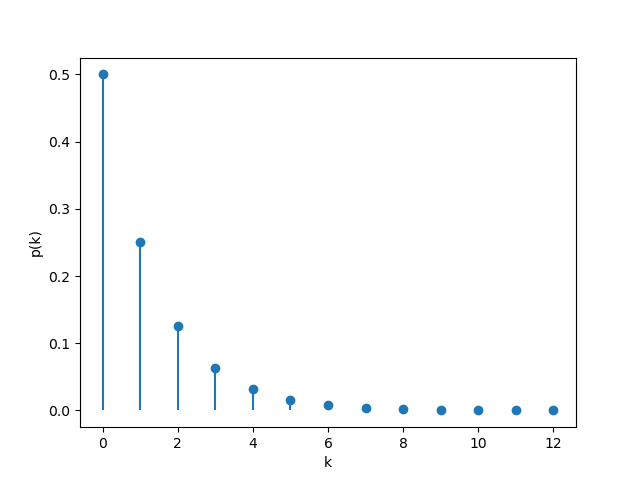
定义发动觉醒技凿险时所需的屯田次数为$X$，并定义一次伯努利试验（Bernoulli trial）的“成功”为判定非♥，而“失败”为判定♥。由此可知，$X$为成功和失败次数之和。若定义成功次数为$r$，则$X$符合负二项分布（Negative binomial distribution）。

概率质量函数（PMF, Probability mass function）:

\[p_{X}(n) = {\binom{n-1}{k}}p^{r}(1-p)^{k}, \quad n = k+r \enspace \text{and} \enspace k \in \{\,0,1,2,\dots\,\}\]

注：此处采用负二项分布的“以失败概率$p$入式”的参数化；即$p$表示判定为♥的概率，$r$表示达到$r$次非♥所需总试验次数。

在此模型下，$r=3, \enspace p=3/4$。

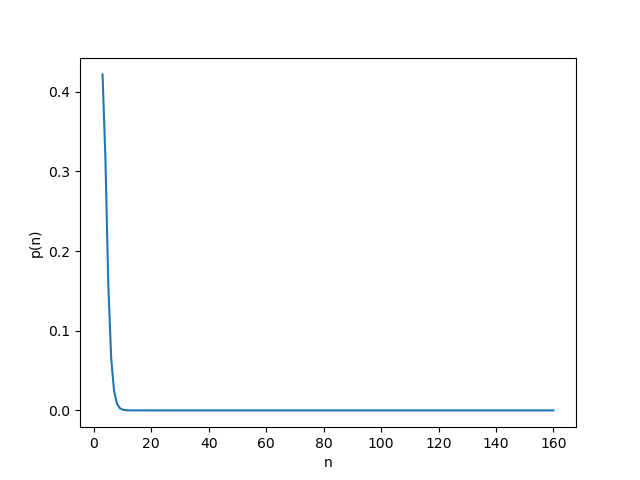
其概率曲线为：

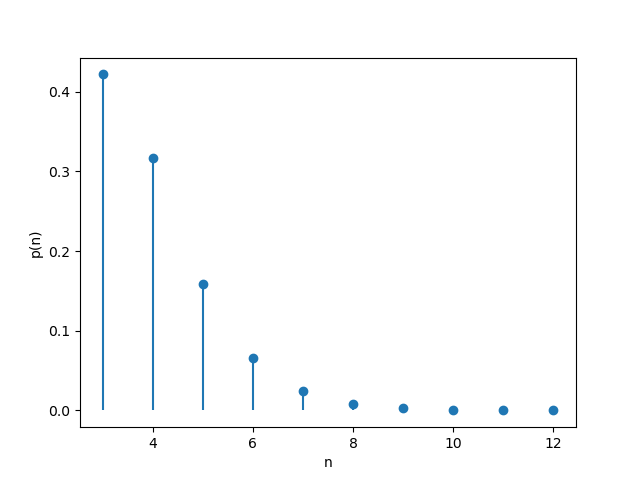
重点观察$n$较小时的概率散点图：

数学期望（Expected value）和方差（Variance）分别为：

\[\boxed{ \mathbb E[X] = \frac{r}{p} = 4 }\] \[\boxed{ \operatorname{Var}(X) = \frac{r(1-p)}{p^{2}} = \frac{4}{3} }\]

这说明在理想情况下，发动觉醒技凿险时所需的屯田次数平均为4次。

【现实模型】

定义发动觉醒技凿险时所需的屯田次数为$X$，牌堆中的牌数为$N$，牌堆中♥的牌数为$K$ ($K \le N$)，并定义一次伯努利试验的“成功”为判定♥，而“失败”为判定非♥（注意：此处为方便使用负超几何分布的标准形式，成功与失败的定义与理想模型下相反）。若定义失败次数为$r$，则成功次数符合负超几何分布（Negative hypergeometric distribution）。

PMF：

\[p_{X}(k)=\frac{\binom{K+r-1}{k}\binom{N-r-K}{K-k}}{\binom{N}{K}}, \quad k=0,1,\dots,K\]

在此模型下，$r=3$。

数学期望和方差分别为：

\[\boxed{ \mathbb E[X] = \frac{rK}{N-K+1}+r = \frac{rN+r}{N-K+1} = \frac{3N+3}{N-K+1} }\] \[\boxed{ \operatorname{Var}(X) = \frac{rK(N+1)(N-K-r+1)}{(N-K+1)^{2}(N-K+2)} = \frac{3K(N+1)(N-K-2)}{(N-K+1)^{2}(N-K+2)} }\]

如果我们假定$K = N/4$，那么：

\[\mathbb E[X] = 4-\frac{4}{3N+4} < 4\] \[\operatorname{Var}(X) = \frac{12N(N+1)(3N-8)}{(3N+4)^{2}(3N+8)}\]

可见，$\mathbb E[X]$与$N$正相关，且小于理想模型下屯田次数的数学期望。

甄姬（标准版）

洛神：回合开始阶段，你可以进行判定：若为♠或♣，立即获得此牌，并可以再次使用洛神——如此反复，直到出现♥或♦为止。

下面我们考虑洛神所获得的牌数。

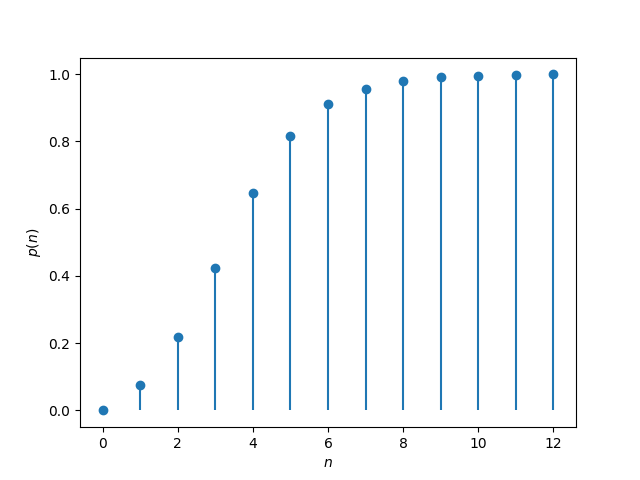
【理想模型】

定义洛神获得的牌数为$Y$，并定义一次伯努利试的“成功”为判定红牌，而“失败”为判定黑牌。很显然，$Y$属于失败次数，且其概率分布符合几何分布（Geometric distribution）的第二种形式。

PMF：

\[p_{Y}(k) = (1-p)^{k}p, \quad k \in \{\,0,1,2,\dots\,\}\]

其中$p$为“失败”的概率，在此模型下$p = 1/2$。

其概率曲线为：

重点观察$k$较小时的概率散点图：

数学期望和方差分别为：

\[\boxed{ \mathbb E[Y] = {\frac{1-p}{p}} = 1 }\] \[\boxed{ \operatorname{Var}(Y) ={\frac {1-p}{p^{2}}} = 2 }\]

这说明在理想情况下，洛神所得的牌数平均为1张。

实际上，几何分布是负二项分布的特殊情况：

\[\operatorname{Geom}(p) = \operatorname{NB}(1,p)\]

我们由此可以发现甄姬洛神和邓艾屯田的内在联系。

接下来我们考察甄姬的Online战功“洛神赋”：使用甄姬一回合内发动洛神在不被改变判定牌的情况下连续判定黑色花色至少8次。

\[p_{Y}(k \ge 8) = 1 - \sum_{k = 0}^7{p_Y(k)} = \frac{1}{256} \approxeq 0.003906\]

【现实模型】

定义洛神获得的牌数仍为$Y$，牌堆中的牌数为$N$，牌堆中红牌数为$K$ ($K \le N$)，并定义一次伯努利试验的“成功”为判定黑牌，而“失败”为判定红牌（注意：此处的定义与理想模型下刚好相反）。我们已经知道几何分布是负二项分布的特例，所以成功次数符合负超几何分布（Negative hypergeometric distribution），且失败次数$r=1$。

数学期望和方差分别为：

\[\boxed{ \mathbb E[Y] = \frac{rK}{N-K+1} = \frac{K}{N-K+1} }\] \[\boxed{ \operatorname{Var}(Y) = \frac{rK(N+1)(N-K-r+1)}{(N-K+1)^{2}(N-K+2)} = \frac{K(N+1)(N-K)}{(N-K+1)^{2}(N-K+2)} }\]

我们也可以通过Stars and bars的方法来直观地得到上述数学期望。设想有$N$个球，其中$K$个为黑色，那么红色球有$N-K$个。把这些红球看作隔板，它们把空间分成了$N-K+1$个区域。每个黑球在某一个区域的概率都相同，为$\frac{1}{N-K+1}$。因此，$K$个黑球在第一个区域的期望为$\frac{K}{N-K+1}$。

如果我们假定$K = N/2$，那么：

\[\mathbb E[Y] = \frac{1}{1+\frac{2}{N}} < 1\] \[\operatorname{Var}(Y) = \frac{N^2(N+1)}{(N+2)(N+4)}\]

可见，$\mathbb E[Y]$与$N$正相关，且小于理想模型下洛神牌的数学期望。

前文对军争篇模型的介绍中已经提到，我们假设某一时刻，牌堆平均有143张牌。那么：

\[\mathbb E_{\text{avg}} = \frac{1}{1+\frac{2}{143}} \approxeq 0.9862\]

孟获（神话再临·林）

再起：摸牌阶段，若你已受伤，你可以放弃摸牌并展示牌堆顶的X张牌，X为你已损失的体力值，其中每有一张♥牌，你回复1点体力，然后弃掉这些♥牌，将其余的牌收入手牌。

接下来我们来研究再起获得的体力值。

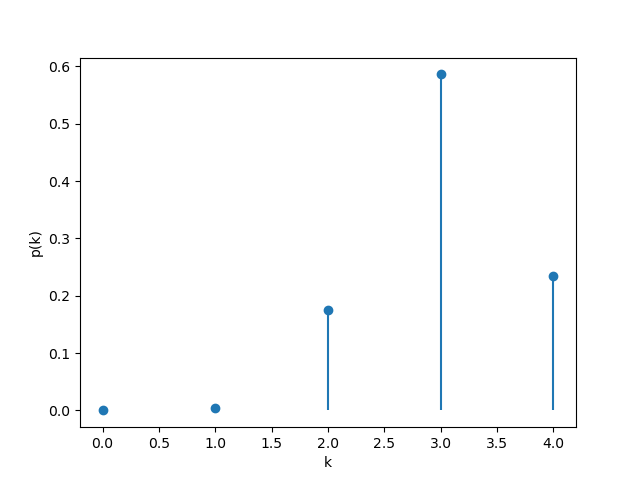
【理想模型】

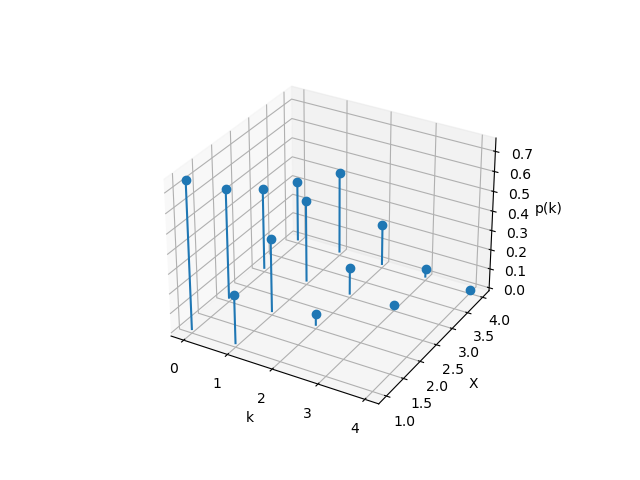
定义在损失$X \enspace (0 < X \le 4)$体力值的情况下，再起所获得的体力值为$H$，并定义一次伯努利试验的“成功”为判定♥，而“失败”为判定非♥。很显然，$H$属于成功次数，且其概率分布符合二项分布（Binomial distribution）$H \sim \operatorname{Bin}(n,p)$。

PMF：

\[p_{H}(k) = {\binom{n}{k}}p^{k}(1-p)^{n-k}, \quad k \in \mathbb{N} \enspace \text{and} \enspace k=0,1,2,\dots,n\]

其中$n$为伯努利试验的次数，$p$为判定为♥的概率。在此模型下，$n=X, \enspace p=1/4$。

其概率散点图为：

以$X = 3$为例：

数学期望和方差分别为：

\[\boxed{\mathbb E[H] = \frac{X}{4}}\] \[\boxed{\operatorname{Var}(H) = np(1-p) = \frac{3X}{16}}\]

同理，定义所获得手牌为$C$，则$C \sim \operatorname{Bin}(X,3/4)$。

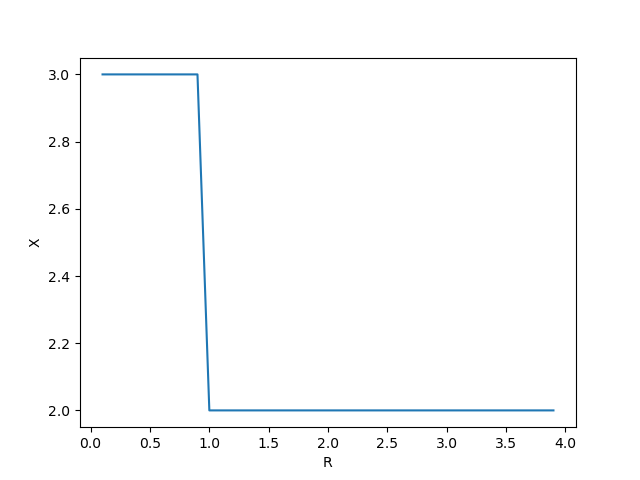
\[\boxed{\mathbb E[C] = \frac{3X}{4}}\] \[\boxed{\operatorname{Var}(C) = np(1-p) = \frac{3X}{16}}\]

这里我们继续讨论一个问题：$X=?$时发动再起收益最高？

我们需要首先定义“收益”的概念。如果认为一点体力值等价于$R$张牌，那么我们可以将再起的收益用牌数来表示：

\[P = C + HR\] \[\mathbb E[P] = \mathbb E[C]+R\mathbb E[H] = \frac{X}{4}(3+R)\]

一般认为，$R \approxeq 2$，即“一血=两牌”理论（郭嘉遗计、黄盖苦肉、钟会排异等都是佐证）。该理论经大量游戏实践验证而一度在玩家中非常流行。当然，不少玩家对此理论也持不同观点，因此我们要讨论在再起技能的情况下，$R$值的合理范围。

如果不发动再起，摸牌阶段会获得$2$张牌。若要使发动再起的收益不劣于不发动，那么：

\[\mathbb E[P] \ge 2\]

所以

\[R \ge \frac{8}{X} - 3\]

上述曲线图如下：

可见：

当$X \ge 3$时，无论$R$值如何，发动再起都有正收益
当$X = 1$时，我们应当认为发动再起应当有负收益，否则玩家可以在该角色受伤时总是选择发动此技能而不会担心带来负收益，而这就意味着此技能设计过强。所以，$R < 5$
当$X = 2$时，如果我们认为发动再起应当有正向收益，那么$R \ge 1$；否则$0 < R \le 2$

综上所述，$R = 2$是一个合理的取值。在此取值下，当$X le 2$时，若非特殊情况，玩家不应发动此技能。

【现实模型】

定义牌堆中的牌数为$N$，牌堆中♥牌数为$K$ ($K \le N$)。在此模型下，伯努利试验是不放回的取样，此时成功次数符合超几何分布（Hypergeometric distribution）$H \sim HG_{N,K,n}(k)$。

PMF：

\[p_{H}(k)=\frac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}}, \quad k \in \{\,0,1,2,\dots\,\} \enspace \text{and} \enspace \max(0,n+K-N)\leq k\leq \min(K,n)\]

其中$n$为伯努利试验的次数，$n=X$。

数学期望和方差分别为：

\[\boxed{\mathbb E[H] = np = Xp}\] \[\boxed{\operatorname{Var}(H) = \frac{np(1-p)(N-n)}{N-1} = \frac{Xp(1-p)(N-X)}{N-1}}\]

其中，$p = K/N$。

如果我们假定$K = N/4$，则$p=1/4$，那么：

\[\mathbb E[H] = \frac{X}{4}\] \[\operatorname{Var}(H) = \frac{3X}{16}\frac{N-X}{N-1} < \frac{3X}{16}\]

实际上，超几何分布和负超几何分布有以下联系：

\[NHG_{N,K,r}(k)=1-HG_{N,N-K,k+r}(r-1)\]

我们由此可以发现孟获再起和邓艾屯田的内在联系。

伯努利试验概率分布小结

以上武将技能分析涵盖了抽样问题的四种概率分布：

	有放回（理想模型）	不放回（军争模型）
抽样数固定时成功数的分布	二项分布再起	超几何分布再起
失败数固定时成功数的分布	负二项分布屯田（特例：几何分布洛神）	负超几何分布屯田洛神

还有几名武将的技能符合以上几种分布，我们简略列举如下。由于分析过程类似，我们将只讨论理想模型而忽略现实模型。

黄月英（标准版）

集智：当你使用普通锦囊牌时，你可以摸一张牌。

假设当前手牌中的普通锦囊牌有$r$张，并定义本回合内可发动集智的次数为$X$（假设每当使用普通锦囊牌时都会发动集智；不考虑【无中生有】和【五谷丰登】的影响），则$X$符合负二项分布：

\[X \sim NB(r,p)\]

其中$p$为判定为非普通锦囊牌的概率。在此模型下，$p=\frac{117}{160}$。

数学期望和方差分别为：

\[\boxed{ \mathbb E[X] = \frac{r}{p} = \frac{160}{117}r \approxeq 1.3675r }\] \[\boxed{ \operatorname{Var}(X) = \frac{r(1-p)}{p^{2}} = \frac{6880}{13689}r \approxeq 0.5026r }\]

袁绍（神话再临·火）

乱击：出牌阶段，你可以将任意两张相同花色的手牌当【万箭齐发】使用。

本节研究当手牌数为$n$时，可以发动乱击的次数。这里采用的方法基于二项分布。

求 $m$ 种花色的 $n$ 张手牌中，最大配对数的期望。

设 $m \ge 2$，$n \in \mathbb{N}$。令

\[X_1, X_2, \dots, X_n\]

为相互独立同分布的随机变量，且

\[\mathbb{P}(X_i = j) = \frac{1}{m}, \quad j = 1,2,\dots,m\]

对每一个取值$j$，定义出现次数

\[N_j := \#\{ i \in \{1,\dots,n\} : X_i = j \}\]

若两个元素取值相同，则可构成一对；每个元素最多只能使用一次。因此，对取值$j$最多能形成的配对数为

\[\left\lfloor \frac{N_j}{2} \right\rfloor\]

整个样本中能形成的最大配对数为

\[P_{\max} := \sum_{j=1}^{m} \left\lfloor \frac{N_j}{2} \right\rfloor\]

目标是计算最大配对数的期望

\[\mathbb{E}[P_{\max}]\]

虽然随机变量 $N_1,\dots,N_m$ 彼此相关，但期望具有线性性，因此

\[\mathbb{E}[P_{\max}] = \sum_{j=1}^{m} \mathbb{E}\!\left[\left\lfloor \frac{N_j}{2} \right\rfloor\right]\]

由于对称性，

\[\mathbb{E}[P_{\max}] = m \, \mathbb{E}\!\left[\left\lfloor \frac{N_1}{2} \right\rfloor\right]\]

注意到

\[N_1 \sim \operatorname{Bin}\!\left(n,\frac{1}{m}\right)\]

对任意整数 $k$，有恒等式

\[\left\lfloor \frac{k}{2} \right\rfloor = \frac{k}{2} - \frac{1}{2}\mathbf{1}_{\{k \text{ 为奇数}\}}\]

因此

\[\mathbb{E}\!\left[\left\lfloor \frac{B}{2} \right\rfloor\right] = \frac{\mathbb{E}[B]}{2} - \frac{1}{2}\mathbb{P}(B \text{ 为奇数}), \quad B \sim \operatorname{Bin}\!\left(n,\frac{1}{m}\right)\]

对于 $B \sim \operatorname{Bin}(n,p)$，有

\[\mathbb{P}(B \text{ 为奇数}) = \frac{1 - (1 - 2p)^n}{2}\]

在此问题中 $p = \frac{1}{m}$，因此

\[\mathbb{P}(B \text{ 为奇数}) = \frac{1 - \left(1 - \frac{2}{m}\right)^n}{2}\]

由于

\[\mathbb{E}[B] = \frac{n}{m}\]

可得

\[\mathbb{E}\!\left[\left\lfloor \frac{B}{2} \right\rfloor\right] = \frac{n}{2m} - \frac{1}{4} + \frac{1}{4}\left(1 - \frac{2}{m}\right)^n\]

最终得到最大配对数的期望：

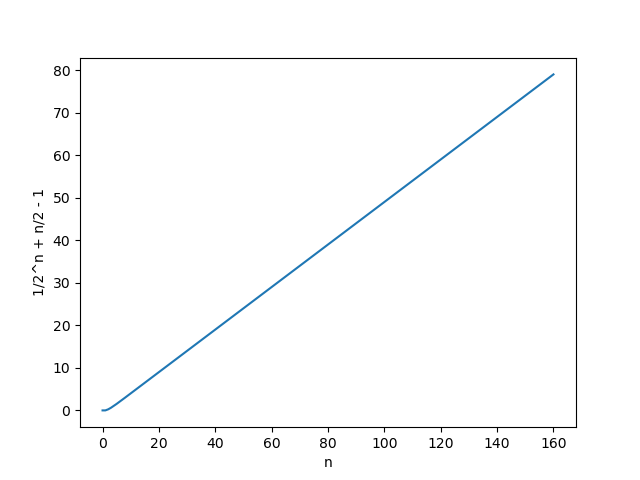
\[\boxed{ \mathbb{E}[P_{\max}] = \frac{n}{2} - \frac{m}{4} + \frac{m}{4}\left(1 - \frac{2}{m}\right)^n }\]

当 $m=4$ 时，

\[\mathbb{E}[P_{\max}] = \frac{n}{2} - \frac{4}{4} + \frac{4}{4}\left(1 - \frac{2}{4}\right)^n = \frac{n}{2} - 1 + \frac{1}{2^{n}}\]

该期望曲线为：

下面计算最大配对数的方差。

对任意整数 $u\ge 0$，有恒等式

\[\left\lfloor\frac u2\right\rfloor=\frac u2-\frac12\mathbf 1_{\{u\text{ 为奇数}\}}\]

因此

\[P_{\max} =\sum_{j=1}^m\left(\frac{N_j}{2}-\frac12\mathbf 1_{\{N_j\text{ 奇}\}}\right) =\frac12\sum_{j=1}^m N_j-\frac12\sum_{j=1}^m \mathbf 1_{\{N_j\text{ 奇}\}} =\frac n2-\frac12\,O\]

其中 $O:=\sum_{j=1}^m I_j,\qquad I_j:=\mathbf 1_{\{N_j\text{ 为奇数}\}}$

于是

\[\operatorname{Var}(P_{\max})=\frac14\,\operatorname{Var}(O)\]

因此关键变成：计算 $O=\sum_{j=1}^m I_j$ 的方差。

注意到对任意整数随机变量 $Y$，有

\[\mathbf 1_{\{Y\text{ 奇}\}}=\frac{1-(-1)^Y}{2}\]

所以

\[\mathbb E[I_1]=\mathbb P(N_1\text{ 奇}) =\frac{1-\mathbb E[(-1)^{N_1}]}{2}\]

而 $N_1\sim\operatorname{Bin}(n,\tfrac1m)$。对于二项分布随机变量，其概率生成函数（Probability-generating function）为

\[\mathbb E[t^{N_1}]=\sum_{k=0}^{n} t^k \binom{n}{k} p^k (1-p)^{n-k} = (1-p+pt)^n,\quad p=\frac1m\]

其中最后一步由二项式定理得到。

取 $t=-1$ 得到

\[\mathbb E[(-1)^{N_1}]=(1-p-p)^n=(1-2p)^n=\left(1-\frac{2}{m}\right)^n\]

定义 $a:=\left(1-\frac{2}{m}\right)^n$，于是

\[\mathbb E[I_1]=\frac{1-a}{2}\]

由于 $I_1$ 是 $0/1$ 变量，有 $I_1^2 = I_1$，因此$\mathbb{E}[I_1^2] = \mathbb{E}[I_1]$

所以

\[\begin{aligned} \operatorname{Var}(I_1) &= \mathbb{E}[I_1^2] - (\mathbb{E}[I_1])^2 \\ &= \mathbb E[I_1](1-\mathbb E[I_1]) \\ &= \frac{1-a}{2}\cdot\frac{1+a}{2} \\ &= \frac{1-a^2}{4} \end{aligned}\]

计算协方差 $\operatorname{Cov}(I_1,I_2)$，需要 $\mathbb E[I_1I_2]$：

\[I_j=\frac{1-(-1)^{N_j}}{2} \quad\Longrightarrow\quad I_1I_2=\frac{1-(-1)^{N_1}-(-1)^{N_2}+(-1)^{N_1+N_2}}{4}\]

取期望：

\[\mathbb E[I_1I_2] =\frac{1-\mathbb E[(-1)^{N_1}]-\mathbb E[(-1)^{N_2}]+\mathbb E[(-1)^{N_1+N_2}]}{4}\]

由对称性 $\mathbb E[(-1)^{N_1}]=\mathbb E[(-1)^{N_2}]=a$，所以

\[\mathbb E[I_1I_2]=\frac{1-2a+\mathbb E[(-1)^{N_1+N_2}]}{4}\]

现在计算 $\mathbb E[(-1)^{N_1+N_2}]$。令 $S:=N_1+N_2.$

由于每张牌的花色独立地以概率 $\frac{1}{m}$ 取每个值，故花色落在 $\{1,2\}$ 的概率为 $\frac{2}{m}$。因此

\[S = N_1 + N_2 \sim\operatorname{Bin}\!\left(n,\frac{2}{m}\right)\]

利用前面的概率生成函数结果（取 $p = \frac{2}{m}$，$t = -1$）：

\[\mathbb E[(-1)^S] =\left(1-2 \cdot \frac{2}{m}\right)^n =\left(1-\frac{4}{m}\right)^n\]

定义 $b:=\left(1-\frac{4}{m}\right)^n$ ，代回得到

\[\mathbb E[I_1I_2]=\frac{1-2a+b}{4}\]

于是

\[\operatorname{Cov}(I_1,I_2) =\mathbb E[I_1I_2]-\mathbb E[I_1]^2 =\frac{1-2a+b}{4}-\left(\frac{1-a}{2}\right)^2 =\frac{b-a^2}{4}\]

因为 $O=\sum_{j=1}^m I_j$，且各 $I_j$ 交换对称，所以

\[\begin{aligned} \operatorname{Var}(O) &= \sum_{j=1}^m \operatorname{Var}(I_j) + \sum_{j \neq k} \operatorname{Cov}(I_j, I_k) \\ &= m\,\operatorname{Var}(I_1)+m(m-1)\,\operatorname{Cov}(I_1,I_2) \end{aligned}\]

代入上面的结果：

\[\operatorname{Var}(O) = m\cdot\frac{1-a^2}{4}+m(m-1)\cdot\frac{b-a^2}{4} =\frac{m}{4}(1-a^2)+\frac{m(m-1)}{4}(b-a^2)\]

因此

\[\boxed{ \operatorname{Var}(P_{\max}) =\frac14\,\operatorname{Var}(O) = \frac{m}{16}(1-a^2)+\frac{m(m-1)}{16}(b-a^2) }\]

其中

\[a=\left(1-\frac{2}{m}\right)^n,\qquad b=\left(1-\frac{4}{m}\right)^n\]

当 $m=4$ 时

\[a=\left(\frac12\right)^n,\qquad b=(1-1)^n=0\quad(n\ge 1)\]

代入得到

\[\operatorname{Var}(P_{\max}) =\frac{4}{16}\left(1-2^{-2n}\right)+\frac{12}{16}\left(0-2^{-2n}\right) =\frac{1}{4}-\frac{1}{4^n}\]

对于袁绍的技能乱击，我们还会研究另一个课题。见“生日问题”一节）。

二次函数

王朗（SP）

鼓舌：出牌阶段限一次，你可以用一张手牌与至多三名角色同时拼点，然后依次结算拼点结果，没赢的角色选择一项：1. 弃置一张牌；2. 令你摸一张牌。若拼点没赢的角色是你，你需先获得一个“饶舌”标记（你有7个“饶舌”标记时，你死亡）。

激词：当你发动“鼓舌”拼点的牌亮出后，若点数小于X，你可令点数+X；若点数等于X，你可以令你本回合发动“鼓舌”的次数上限+1。（X为你“饶舌”标记的数量）

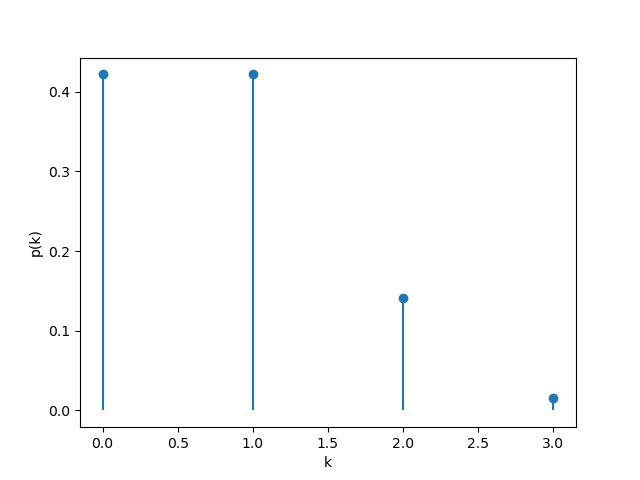
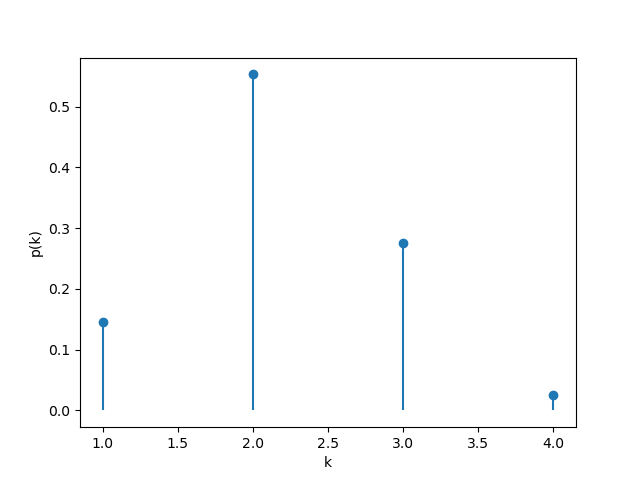
下面考察发动激词的情况下拼点赢的概率。定义王朗玩家的拼点牌点数为$T$，“饶舌”标记数量为$x$，则拼点赢的可能情况数为：

\[C_{T,x} = \min\{13,\; T + x\mathbf{1}_{\{T<x\}}\} - 1\]

拼点赢的概率：

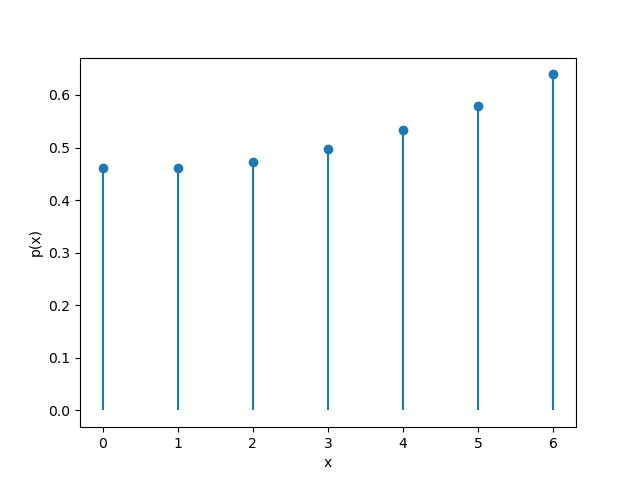
\[\begin{aligned} p(x) &= \mathbb E_T\!\left[\mathbb P\!\left(U < T + \mathbf{1}_{\{T<x\}}x \mid T\right)\right] \\ &= \frac{1}{13}\sum_{T=1}^{13}\frac{C_{T,x}}{13} \\ &= \frac{1}{169}\left(\sum_{i=1}^{x-1}(i+x-1)+\sum_{i=x}^{13}(i-1)\right) \\ &= \frac{x^2-x+78}{169} \end{aligned}\]

其中$U$表示对手的拼点牌点数，$0 \le x \le 6$。

由于对$T<x$的区间求和产生了等差数列求和项，故$p(x)$关于$x$为二次函数。

其概率散点图如下：

可见，随着“饶舌”标记的增多，拼点赢的概率连续增大。

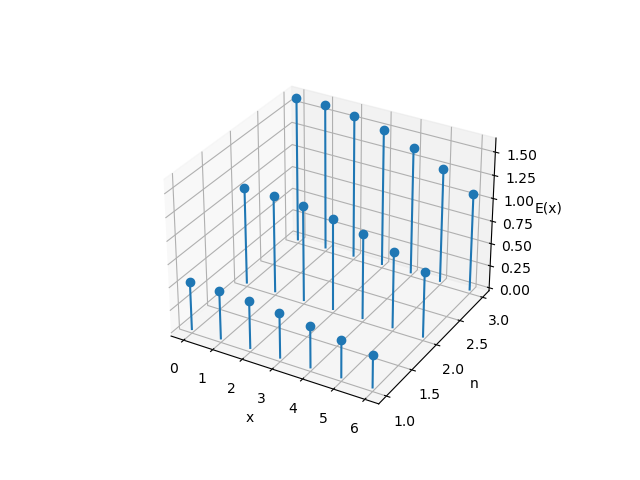
接下来研究“饶舌”标记数量为$x$时，发动鼓舌而获得的“饶舌”标记数量$K$。假设发动鼓舌时与$n$名角色同时拼点，其中$0 < n \le 3$。很明显，其概率符合二项分布$K \sim \operatorname{Bin}(n,1-p(x))$，数学期望和方差分别为：

\[\boxed{\mathbb E[K;x] = n(1-p(x)) = \frac{n}{169}(91-x^2+x)}\] \[\boxed{ \begin{aligned} \operatorname{Var}(K;x) &= np(x)(1-p(x)) \\ &= \frac{n}{28561}(91-x^2+x)(x^2-x+78) \\ &= \frac{n}{28561}(-x^4+2x^3+12x^2-13x+7098) \end{aligned} }\]

其期望散点图如下：

以$n = 3$为例：

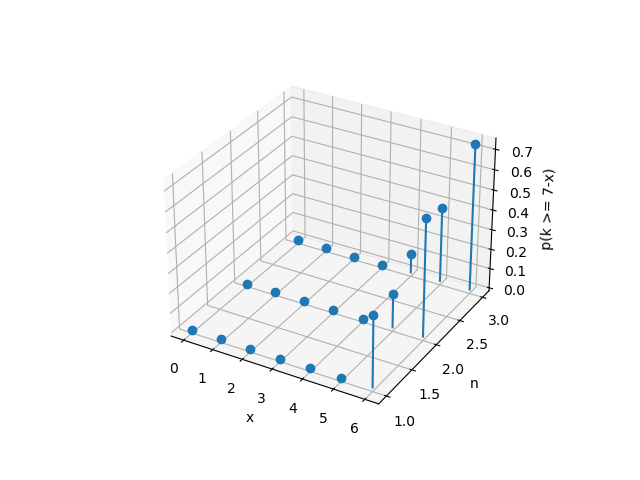
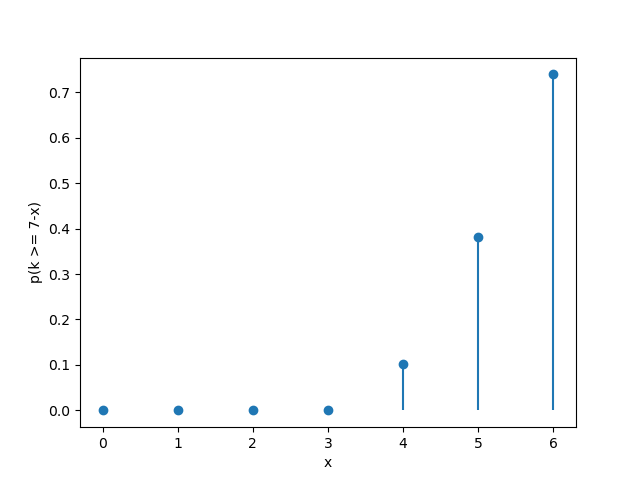
最后，计算发动鼓舌后角色死亡的概率：

\[\mathbb{P}(K \ge 7-x) = 1-\mathbb{P}(K \le 6-x) = 1-F(6-x;n;1-p(x)) = 1-\sum_{i=0}^{6-x}\binom{n}{i}(1-p(x))^{i}p(x)^{n-i}\]

其中$F$为累积分布函数（Cumulative distribution function）。

\[\begin{aligned} \mathbb{P}(K \ge 7-x) = \begin{cases} 0 & \text{if $x \le 6-n$} \\ 1-\frac{1}{169^{n}}\sum_{i=0}^{6-x}\binom{n}{i}(91-x^2+x)^{i}(x^2-x+78)^{n-i} & \text{otherwise} \end{cases} \end{aligned}\]

其概率散点图如下：

以$n = 3$为例：

生日问题

孙资&刘放（原创之魂2016）

（图片来源：https://www.bilibili.com/read/cv16369119）

瑰藻：若你于弃牌阶段弃置过至少两张牌且这些牌花色均不相同，则你可以回复1点体力或摸一张牌。

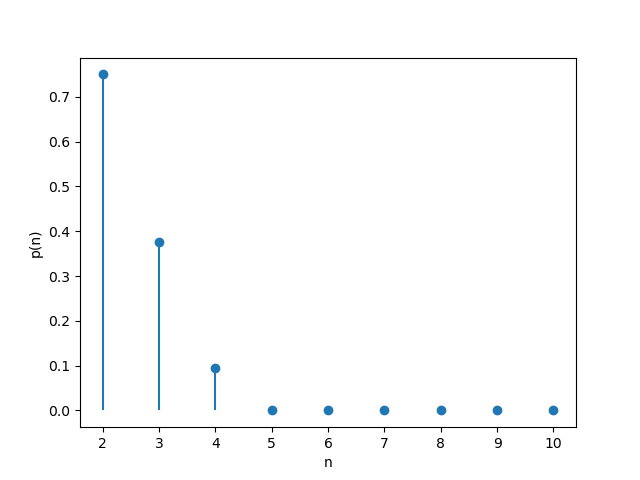
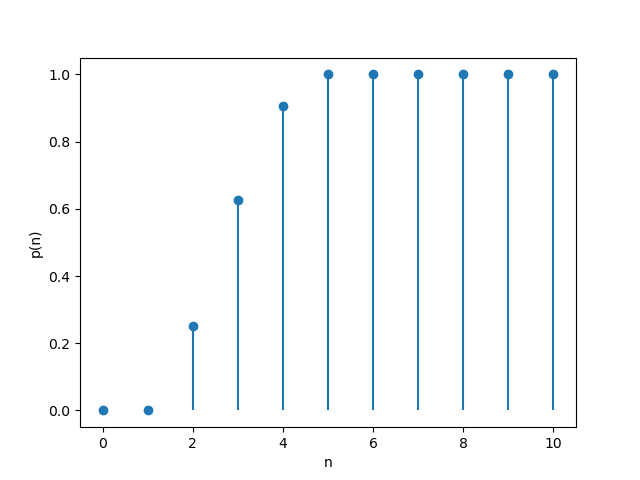
下面我们来计算瑰藻可以回复体力或摸牌的概率。

定义弃牌阶段弃置的牌数为$n \enspace (n > 1)$，一副牌中不同的花色数为$m$。在理想模型下，可将弃置牌的花色近似视为独立均匀分布于$m$类。此问题为典型的生日问题（Birthday problem）：

\[{\bar {p}}(n) = \frac{m!}{(m-n)!m^{n}}, \quad 1 < n \le m\]

根据鸽巢原理（Pigeonhole principle），当$n > m$时，${\bar {p}}(n) = 0$。

在此模型下，$m=4$。

其概率散点图为：

周泰（神话再临·风）

（图片来源：https://www.bilibili.com/read/cv15635764）

不屈：锁定技，当你处于濒死状态时，你将牌堆顶的一张牌置于你的武将牌上，称为“创”，若此牌的点数与已有的“创”点数均不同，则你将体力回复至1点。若出现相同点数则将此牌置入弃牌堆，若你的武将牌上有“创”，则你的手牌上限与“创”的数量相等。

我们考虑不屈失败时的“创”数。定义$X$为出现首次点数重复所需翻牌次数（包含触发重复的那一次），一副牌中不同的点数为$M$。此问题可用生日问题的一种形式来描述。

PMF：

\[p_{X}(k) = \frac{m!(k-1)}{m^{k}(m-k+1)!}, \quad k \in \mathbb{Z} \enspace \text{and} \enspace 1 \le k \le m + 1\]

在此模型下，$m=13$。

其概率散点图为：

数学期望为：

\[\boxed{ \mathbb E[X] = 1 + \sum_{k=1}^{m}{\frac{m!}{(m-k)!m^{k}}} \approxeq 5.2124 }\]

我们也可以将右式进行拉马努金渐近展开，从而得到简化的近似表达式：

\[\mathbb E[X] \sim \sqrt{\frac{\pi m}{2}}+\frac {2}{3} \approxeq 5.1856\]

由此我们可知，周泰的“创”数平均约为5.2张。

接下来我们考察周泰的Online战功“金枪不倒”：使用周泰在一局游戏中拥有过至少9张“不屈”牌并且未死。

\[p_{X}(k \ge 9) = 1 - \sum_{k = 2}^8{p_X(k)} \approxeq 0.06361\]

【点数非均匀修正】

若考虑【2】与【Q】的概率较于其他点数略高，我们可以对PMF做细微修正，得到更加准确的数学期望：

\[\mathbb E[X] \approxeq 5.2065\]

可见，此结果的差异完全可以忽略。

神吕蒙（神话再临·风）

涉猎：摸牌阶段，你可选择采取以下行动来取代摸牌：从牌堆顶亮出五张牌，拿走不同花色的牌各一张，弃掉其余的。

下面我们研究涉猎获得的牌数$X$。该问题是生日问题的一种形式。根据第二类斯特林数（Stirling numbers of the second kind）的定义：

PMF：

\[p_{X}(k) = \frac{m^{\underline k}}{m^{n}}\begin{Bmatrix}n\\k\end{Bmatrix}\]

其中$n$为亮出的牌数，$m$为一副牌中不同的花色数。在此模型下，$n=5, \enspace m=4$。

其概率散点图为：

数学期望和方差分别为：

\[\boxed{ \mathbb E[X] = m(1-(1-\frac{1}{m})^n) = \frac{781}{256} \approxeq 3.0508 }\] \[\boxed{ \operatorname{Var}(X) = m(m-1)(1-\frac{2}{m})^{n}+m(1-\frac{1}{m})^{n}-m^2(1-\frac{1}{m})^{2n} = \frac{27735}{65536} \approxeq 0.4232 }\]

袁绍（神话再临·火）

对于袁绍的技能乱击，除了前面提到的最大配对数，我们还可以研究发动乱击的概率。

定义手牌数为$X$，一副牌中不同的花色数为$m$。可以发动乱击的概率可用生日问题的另一种形式来表示：

\[p_{X}(n) = 1-\prod_{k=1}^{n-1}\left(1-{\frac{\min(k, m)}{m}}\right)\]

在此模型下，$m=4$。当$n \ge 5$时，$p_{X}(n) = 1$。

其概率散点图为：

和约束下可选子集最大规模的期望

曹冲（新一将成名2013）

（图片来源：https://www.bilibili.com/read/cv15576366）

称象：当你受到伤害后，你可以亮出牌堆顶的四张牌，然后你获得其中的任意张点数之和不大于13的牌。

下面我们考虑理想模型下称象获得的牌数。

【Ehrhart】

用 $\mathbf{x} = (x_1,x_2,x_3,x_4)^{\mathsf T},\qquad x_i \in \{\,1,2,\dots\,\}$ 表示亮出的四张牌的点数。定义随机变量$K$为称象最终获得的牌数，即满足点数和不超过 13 的可选牌张数。

【情形一】

当$K = 4$时，四张牌全部可取，需满足

\[x_1+x_2+x_3+x_4 \le 13\]

运用Stars and bars法，可知其整数解组数为

\[\binom{13}{4} = 715\]

【情形二】

当$K = 1$时，当且仅当恰有一张牌可取，对应的不等式系统可写为

\[A\mathbf x\le \mathbf b\]

其中

\[A=\begin{pmatrix} -1 & -1 & 0 & 0 \\ -1 & 0 & -1 & 0 \\ -1 & 0 & 0 & -1 \\ 0 & -1 & -1 & 0 \\ 0 & -1 & 0 & -1 \\ 0 & 0 & -1 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}, \qquad \mathbf b= \begin{pmatrix} -14\\-14\\-14\\-14\\-14\\-14\\ 13\\13\\13\\13\\ -1\\-1\\-1\\-1 \end{pmatrix}\]

该不等式组定义了一个四维凸多胞形（Convex polytope）。问题等价于计算该多胞形中晶格点的数量。以上矩阵不等式为该四维凸多胞形的半空间表示（Half-space representation）。利用开源软件polymake计算可知，该凸多胞形为整多胞形（Integral polytope），其Ehrhart多项式（Ehrhart polynomial）：

  
polytope > $p = new Polytope(INEQUALITIES=>[[-14,1,1,0,0],[-14,1,0,1,0],[-14,1,0,0,1],[-14,0,1,1,0],[-14,0,1,0,1],[-14,0,0,1,1],[-1,1,0,0,0],[-1,0,1,0,0],[-1,0,0,1,0],[-1,0,0,0,1],[13,-1,0,0,0],[13,0,-1,0,0],[13,0,0,-1,0],[13,0,0,0,-1]]);

polytope > print $p->LATTICE;
true

polytope > print $p->EHRHART_POLYNOMIAL;
2592*x^4 + 1296*x^3 + 252*x^2 + 24*x + 1

因此，该凸多胞形内晶格点的个数为

\[\#(K=1)=2592+1296+252+24+1=4165\]

【情形三】

当$K = 3$时，根据不可取牌在四个位置中的不同分布情况，可将可行域划分为若干互不相交的情形。每一种情形均可表示为一个线性不等式系统

\[A_i \mathbf x \le \mathbf b_i\]

从而对应一个四维凸多胞形。

\[A_1 = \begin{pmatrix} -1 & -1 & -1 & -1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}, \qquad \mathbf b_1 = \begin{pmatrix} -14 \\ 13 \\ 13 \\ 13 \\ 13 \\ -1 \\ -1 \\ -1 \\ -1 \end{pmatrix}\] \[A_2 = \begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & -1 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}, \qquad \mathbf b_2 = \begin{pmatrix} 13 \\ 13 \\ 13 \\ -14 \\ -1 \\ -1 \\ -1 \\ -1 \end{pmatrix}\] \[A_3 = \begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ -1 & 0 & -1 & -1 \\ 0 & -1 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}, \qquad \mathbf b_3 = \begin{pmatrix} 13 \\ 13 \\ -14 \\ -14 \\ -1 \\ -1 \\ -1 \\ -1 \end{pmatrix}\] \[A_4 = \begin{pmatrix} -1 & -1 & -1 & -1 \\ 1 & 1 & 1 & 0 \\ -1 & -1 & 0 & -1 \\ -1 & 0 & -1 & -1 \\ 0 & -1 & -1 & -1 \\ 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}, \qquad \mathbf b_4 = \begin{pmatrix} -14 \\ 13 \\ -14 \\ -14 \\ -14 \\ 13 \\ -1 \\ -1 \\ -1 \\ -1 \end{pmatrix}\]

上述四个不等式系统分别给出了四个四维凸多胞形。

由牌位的对称性可知，其对应的组合系数分别为：$\binom{4}{4} = 1$、$\binom{4}{3} = 4$、$\binom{4}{2} = 6$和$\binom{4}{1} = 4$。

再次利用polymake的计算可知，以上四种情况对应的四个凸多胞形均为有理多胞形（Rational polytope）而非整多胞形。因此，只能通过求解其Ehrhart准多项式（Ehrhart quasi-polynomial）来求解其所包含的晶格点：

  
polytope > $p1 = new Polytope(INEQUALITIES=>[[-14,1,1,1,1],[13,-1,-1,-1,0],[13,-1,-1,0,-1],[13,-1,0,-1,-1],[13,0,-1,-1,-1],[-1,1,0,0,0],[-1,0,1,0,0],[-1,0,0,1,0],[-1,0,0,0,1]]);

polytope > $p2 = new Polytope(INEQUALITIES=>[[13,-1,-1,-1,0],[13,-1,-1,0,-1],[13,-1,0,-1,-1],[-14,0,1,1,1],[-1,1,0,0,0],[-1,0,1,0,0],[-1,0,0,1,0],[-1,0,0,0,1]]);

polytope > $p3 = new Polytope(INEQUALITIES=>[[13,-1,-1,-1,0],[13,-1,-1,0,-1],[-14,1,0,1,1],[-14,0,1,1,1],[-1,1,0,0,0],[-1,0,1,0,0],[-1,0,0,1,0],[-1,0,0,0,1]]);

polytope > $p4 = new Polytope(INEQUALITIES=>[[13,-1,-1,-1,0],[-14,1,1,0,1],[-14,1,0,1,1],[-14,0,1,1,1],[-1,1,0,0,0],[-1,0,1,0,0],[-1,0,0,1,0],[-1,0,0,0,1],[13,0,0,0,-1]]);


polytope > print $p1->LATTICE;
false
polytope > print $p2->LATTICE;
false
polytope > print $p3->LATTICE;
false
polytope > print $p4->LATTICE;
false


polytope > print $p1->EHRHART_QUASI_POLYNOMIAL;
1250/9*x^4 + 1750/9*x^3 + 1675/18*x^2 + 35/2*x + 1
1250/9*x^4 + 1750/9*x^3 + 1675/18*x^2 + 35/2*x + 10/9
1250/9*x^4 + 1750/9*x^3 + 1675/18*x^2 + 35/2*x + 1

polytope > print $p2->EHRHART_QUASI_POLYNOMIAL;
256/9*x^4 + 512/9*x^3 + 352/9*x^2 + 32/3*x + 1
256/9*x^4 + 512/9*x^3 + 352/9*x^2 + 32/3*x + 8/9
256/9*x^4 + 512/9*x^3 + 352/9*x^2 + 32/3*x + 1

polytope > print $p3->EHRHART_QUASI_POLYNOMIAL;
729/8*x^4 + 243/2*x^3 + 117/2*x^2 + 12*x + 1
729/8*x^4 + 243/2*x^3 + 117/2*x^2 + 12*x + 7/8

polytope > print $p4->EHRHART_QUASI_POLYNOMIAL;
5875/9*x^4 + 4400/9*x^3 + 1240/9*x^2 + 53/3*x + 1
5875/9*x^4 + 4400/9*x^3 + 1240/9*x^2 + 53/3*x + 8/9
5875/9*x^4 + 4400/9*x^3 + 1240/9*x^2 + 53/3*x + 1


polytope > print $p1->N_LATTICE_POINTS;
445
polytope > print $p2->N_LATTICE_POINTS;
136
polytope > print $p3->N_LATTICE_POINTS;
284
polytope > print $p4->N_LATTICE_POINTS;
1298

在乘以相应的系数后，此类整数解组数为

\[\#(K=3) = 445+136*4+284*6+1298*4=7885\]

【情形四】

当$K = 2$时，由于所有点数组合的总数为 (13^4)，可通过补集直接得到

\[\#(K=2)=13^4-\#(K=1)-\#(K=3)-\#(K=4)=15796\]

由上述计数结果可得随机变量$K$的概率分布。其概率散点图为：

数学期望和方差分别为：

\[\boxed{\mathbb E[K] = \frac{62272}{28561} \approxeq 2.1803}\] \[\boxed{\operatorname{Var}(K) = \frac{399322010}{815730721} \approxeq 0.4895}\]

该问题亦可通过组合生成函数（Generating function）与次序统计量进行纯组合论推导（参见附录）。但在本问题规模下，该方法并不能显著降低计算复杂度；相反，将计数问题转化为凸多胞形中的晶格点计数，并借助 Ehrhart 理论与 polymake 实现自动化计算，更有利于保证结果的完整性与可复现性。

随机子集和的可达性概率

糜竺（SP）

资援：出牌阶段限一次，你可以将任意张点数之和为13的手牌交给一名其他角色，然后该角色回复1点体力。

下面研究在手牌数为 $X$ 的情况下，可以发动资援的概率。这是典型的NP完备（NP-Complete）的子集和问题（Subset sum problem）。但在手牌数和目标和都固定的情况下，存在多项式时间的算法，其程序如下：

  
from collections import defaultdict
from math import gcd


def subset_sum_probability(n, target=13, max_value=13):
    """
    Computes the exact probability that among n i.i.d. draws from {1,2,...,max_value},
    there exists a nonempty subset whose sum equals `target`.

    Args:
        n: Number of draws
        target: Target sum (default 13)
        max_value: Maximum value per draw (default 13)

    Returns:
        (numerator, denominator): Reduced fraction representing the probability

    Core idea:
    - Track which subset sums (0..target) are achievable so far using a bitmask.
    - Use dynamic programming over masks.
    """

    # We only care about subset sums from 0 to `target`
    # Bit i in the mask means "sum i is achievable"
    WIDTH = target + 1
    FULL_MASK = (1 << WIDTH) - 1
    TARGET_BIT = 1 << target

    # Precompute state transitions
    # next_mask[mask][x] = new mask after adding value x
    # Transition: new_sums = old_sums ∪ (old_sums + x)
    next_mask = [[0] * (max_value + 1) for _ in range(FULL_MASK + 1)]
    for mask in range(FULL_MASK + 1):
        for x in range(1, max_value + 1):
            shifted = (mask << x) & FULL_MASK
            next_mask[mask][x] = mask | shifted

    # DP state: mask where bit k means "sum k is achievable"
    # dp[mask] = count of sequences producing this mask
    # Initially only sum 0 is achievable (mask = 1)
    dp = [0] * (FULL_MASK + 1)
    dp[1] = 1

    # Main DP loop: add one draw at a time
    for _ in range(n):
        new_dp = [0] * (FULL_MASK + 1)

        for mask, count in enumerate(dp):
            if count == 0:
                continue

            row = next_mask[mask]
            for x in range(1, max_value + 1):
                new_mask = row[x]
                new_dp[new_mask] += count

        dp = new_dp

    # Count successful sequences: those with TARGET_BIT set
    numerator = sum(
        count for mask, count in enumerate(dp)
        if mask & TARGET_BIT
    )

    denominator = max_value ** n

    g = gcd(numerator, denominator)
    return numerator // g, denominator // g

该程序的时间复杂度为 $\mathcal{O}(n \cdot 2^{T+1} \cdot m)$，空间复杂度为 $\mathcal{O}(2^{T+1})$。其中 $T$ 为目标和（$13$），$m$为卡牌最大值（$13$）。

其概率曲线为：

重点观察$n$较小时的概率散点图：

【封闭形式】

下面来说明该概率必然存在封闭形式（Closed-form Expression）.

我们研究的是概率

\[p_n = \mathbb{P}\Big( \exists\, I\subseteq\{1,\dots,n\},\ I\neq\varnothing: \sum_{i\in I} X_i = 13 \Big)\]

其中, $X_i$ 独立同分布，取值于 ${1,\dots,13}$

核心问题是：是否存在某个子集和等于 13。这个“是否存在”的判定，并不依赖于所有历史细节，而只依赖于一件事：当前已经“可达”的子集和有哪些（在 0 到 13 之间）

定义状态：

\[R_n := \{\text{前 } n \text{ 个数能组成的所有子集和}\}\cap\{0,1,\dots,13\}\]

每个状态可以用一个 14 位二进制掩码（bitmask）表示。第 $k$ 位为 1 表示“子集和 $k$ 是可达的”。那么，总状态数最多为：

\[2^{14} = 16384\]

即，状态空间是一个有限集合。

当加入第 $n+1$ 个随机变量 $X_{n+1}=x$ 时，状态更新规则是：

\[R_{n+1} = R_n \;\cup\; \{ r+x : r\in R_n,\ r+x\le 13 \}\]

该规则只依赖于 $s$ ，与 $n$ 无关。其随机性只来自输入 $x$，且 $x$ 的分布在每一步都是相同的（均匀分布）。

因此，这是一个有限状态、时间齐次的马尔可夫链（Time-homogeneous Markov chain with a finite state space）。进而我们知道，该概率值必然存在封闭形式。

下面举两个封闭形式的例子：

一、有限维线性递推

由于状态空间有限，状态转移可表示为有限维线性系统。状态演化可以写成

\[\mathbf{v}_{n+1} = \mathbf{v}_n P\]

其中，$\mathbf{v}_n$ 为状态分布向量（有限维）， $P$ 为固定的转移矩阵，且其维数不超过状态数上界 $d$。

由Cayley–Hamilton 定理，矩阵 $P$ 满足其特征多项式，从而存在 $L<\infty$ 和常数 $c_1,\dots,c_L$，使得对所有 $n\ge L$，$p_n$ 满足如下线性递推关系：

\[p_n = c_1 p_{n-1} + \cdots + c_L p_{n-L} \quad (n \ge L)\]

二、生成函数是有理函数

定义生成函数：

\[G(z) = \sum_{n\ge 0} p_n z^n\]

由于 $p_n$ 满足有限阶、常系数线性递推关系，其生成函数必为有理函数，即

\[G(z) = \frac{A(z)}{B(z)}\]

其中 $A(z),B(z)$ 为多项式，且 $B(z)$ 的次数等于递推关系的阶数。

上述有理性也可从向量生成函数的角度理解：由

\[\mathbf v_{n+1}=\mathbf v_nP\]

可得

\[\sum_{n\ge 0}\mathbf v_n z^n=\mathbf v_0(I-zP)^{-1}\]

从而 $\mathbf v_n$ 的任意线性函数（例如 $p_n$）的生成函数皆为有理函数。

【单调性和极限】

可以发动资援的概率随着手牌数单调递增，且其极限为$1$。

命题1

令

\[E_n := \Big\{\exists\, I\subseteq\{1,2,\dots,n\},\ I\neq\varnothing:\ \sum_{i\in I}X_i = 13\Big\}, \qquad p_n := \mathbb{P}(E_n)\]

其中 $X_1,X_2,\dots$ 为独立同分布随机变量，且

\[X_i \sim \mathrm{Unif}\{1,2,\dots,13\}\]

则序列 $(p_n)_{n\ge 1}$ 严格单调递增，即

\[p_{n+1} > p_n \quad \text{对所有 } n\ge 1 \text{成立}\]

证明

首先注意到对任意 $n$，都有集合包含关系

\[E_n \subseteq E_{n+1}\]

因此由概率单调性原理或测度单调性（Measure Monotonicity），

\[p_n \le p_{n+1}\]

下面证明不等号是严格的。

考虑如下事件：

\[B_n := \Big\{ \sum_{i\in I} X_i \neq 13 \text{ 对所有 } I\subseteq\{1,\dots,n\},\ I\neq\varnothing, \ \text{但 } X_{n+1}=13 \Big\}\]

在事件 $B_n$ 中：

前 $n$ 个随机变量无法组成和为 $13$ 的子集，因此 $E_n$ 不发生；
但由于 $X_{n+1}=13$，取单元素集合 ${n+1}$ 即可得到和为 $13$ ，因此 $E_{n+1}$ 发生。

故

\[B_n \subseteq E_{n+1}\setminus E_n\]

由于

\[\mathbb{P}(B_n) = \mathbb{P}\big(X_{n+1}=13\big)\, \mathbb{P}\big(E_n^c\big) = \frac{1}{13}\,\mathbb{P}(E_n^c) > 0\]

（注意 $\mathbb{P}(E_n^c)>0$，例如当 $X_1=\cdots=X_n=2$ 时，任意非空子集和都是偶数，不可能等于 $13$，所以 $E_n^c$ 必然发生），

因此

\[\mathbb{P}(E_{n+1}) - \mathbb{P}(E_n) = \mathbb{P}(E_{n+1}\setminus E_n) \ge \mathbb{P}(B_n) > 0\]

从而

\[p_{n+1} > p_n \tag*{$\square$}\]

命题2

\[\lim_{n\to\infty} p_n = 1\]

证明

定义事件

\[A_n := \{\exists\, i\in\{1,\dots,n\}: X_i = 13\}\]

若 $A_n$ 发生，则取单元素集合 $I={i}$ 就有$\sum_{j\in I}X_j = X_i = 13$，因此

\[A_n \subseteq E_n\]

于是

\[p_n = \mathbb{P}(E_n) \ge \mathbb{P}(A_n)\]

接下来计算 $\mathbb{P}(A_n)$。由于各 $X_i$ 独立且$\mathbb{P}(X_i\neq 13)=\frac{12}{13}$，有

\[\mathbb{P}(A_n) = 1-\mathbb{P}(\forall i,\ X_i\neq 13) = 1-\left(\frac{12}{13}\right)^n\]

另一方面显然 $p_n\le 1$（因为是概率），因此得到夹逼不等式

\[1-\left(\frac{12}{13}\right)^n \le p_n \le 1\]

当 $n\to\infty$ 时， $\left(\frac{12}{13}\right)^n \to 0$，从而左端趋于 $1$。由夹逼定理（Squeeze Theorem）可得

\[\lim_{n\to\infty} p_n = 1 \tag*{$\square$}\]

从另一个角度看，可达子集和集合的演化构成一个有限状态、时间齐次的吸收型马尔可夫链（Absorbing Markov Chain）。所有包含目标值 $13$ 的状态都是吸收态，一旦进入便无法离开。由于从初始状态出发进入吸收态的概率为正，且不存在非吸收的封闭类，该链以概率 $1$ 最终被吸收。因此，目标事件的概率 $p_n$ 随 $n$ 增大必然趋于 $1$。

技能比较

最后，我们在理想模型下比较一些类似的技能。

额外摸牌

	英姿	闭月	洛神	涉猎	再起
期望	1	1	1	1.0508	0.25X
方差	0	0	2	0.4232	0.1875X

注1：再起中的$X$表示已损失体力值。注2：方差越大表示收益波动越大，越不稳定。

英姿和闭月带来稳定的额外摸牌收益
洛神、涉猎和再起的额外摸牌不稳定
洛神、涉猎和再起的额外摸牌受到花色条件的约束
涉猎和再起需要亮出所得的牌
再起的摸牌数一般小于1，但有一定概率可以回复体力

受到伤害后摸牌

	遗计	称象
期望	2	2.1803
方差	0	0.4895

遗计的摸牌数稳定
称象的期望略高，但摸牌数不稳定
称象的摸牌有点数的限制

总结

以上几个同类技能各有优劣，可见设计是比较均衡的。

附录

称象获得牌数的组合生成函数解法

另一种解法从组合生成函数出发，将“无序多重集合计数”与“有序四元组计数”通过一个明确的升标号算子连接起来。该方法完全白盒，且所有计算均归结为有限次系数抽取与有限求和。

设四张牌点数为

\[x_1,x_2,x_3,x_4\in\{1,2,\dots,13\}\]

并记其排序后的次序统计量为

\[A_1\le A_2\le A_3\le A_4\]

定义在总和不超过 $13$ 的约束下最多可取的张数

\[K:=\max\{k\in\{1,2,3,4\}:A_1+\cdots+A_k\le 13\}\]

显然

\[\mathbb P(K\ge k)=\mathbb P(A_1+\cdots+A_k\le 13)\]

并且

\[\mathbb P(K=k)=\mathbb P(K\ge k)-\mathbb P(K\ge k+1)\]

因此，只需分别计数事件 $K\ge 2$、$K\ge 3$、$K\ge 4$ 对应的有序四元组数量。

多重集合的单项式表示

引入形式变量 $y_1,\dots,y_{13}$，用于标记各点数的出现情况。

对任意大小为 $4$ 的多重集合

\[M=\{1^{m_1}2^{m_2}\cdots 13^{m_{13}}\},\qquad \sum_{j=1}^{13}m_j=4\]

其中 $m_j$ 表示点数 $j$ 在多重集合中的重数（出现次数）。定义其对应单项式

\[y^M:=\prod_{j=1}^{13}y_j^{m_j}\]

例：多重集合 ${1,1,2,5}$ 对应 $m_1=2, m_2=1, m_5=1$（其余 $m_j=0$），其单项式为 $y_1^2 y_2 y_5$。

升标号算子

升标号（Labeling）是指将无序的多重集合分配到有序的位置上。

定义升标号线性算子 $\mathrm{Lab}_4$，其在基单项式上的作用为

\[\mathrm{Lab}_4\!\left(\prod_{j=1}^{13}y_j^{m_j}\right) :=\frac{4!}{\prod_{j=1}^{13}m_j!}\prod_{j=1}^{13}y_j^{m_j}, \qquad \sum m_j=4\]

并线性延拓。

组合意义：系数 $\dfrac{4!}{\prod m_j!}$ 正是多项式系数（multinomial coefficient）

\[\binom{4}{m_1, m_2, \dots, m_{13}} = \frac{4!}{\prod_{j=1}^{13} m_j!}\]

它计算的是将该多重集合的 $4$ 个元素分配到 $4$ 个有区分的位置上的排列数。

例：多重集合 ${1,1,2}$ 的升标号系数为 $\dfrac{3!}{2!\cdot 1!}=3$，对应的 $3$ 个有序排列为 $(1,1,2), (1,2,1), (2,1,1)$。

从多重集合到有序四元组的计数

对于任一仅依赖多重集合（即对置换对称）的性质 $\mathcal P$，定义多重集合枚举多项式

\[U_{\mathcal P}(y_1,\dots,y_{13}) :=\sum_{\substack{M:\ \sum m_j=4\\ \mathcal P(M)\ \text{成立}}} y^M\]

则满足性质 $\mathcal P$ 的有序四元组数量为

\[\#\{(x_1,x_2,x_3,x_4):\mathcal P\} = \Big(\mathrm{Lab}_4(U_{\mathcal P})\Big)\Big|_{y_1=\cdots=y_{13}=1}\]

构造 $K\ge k$ 的多重集合枚举多项式

按第 $k$ 小值分层

事件 $K\ge k$ 等价于 $A_1+A_2+\cdots+A_k\le 13$，这仅依赖多重集合结构。

按第 $k$ 小值 $A_k=c$ 进行分层。对于固定的 $c\in{1,2,\dots,13}$：

前 $k$ 张牌满足 $A_1\le A_2\le \cdots \le A_k = c$，即都取自 ${1,\dots,c}$ 且最大值恰为 $c$
第 $k$ 张牌之后的牌（若有）满足 $\ge c$

生成函数构造

为了用生成函数同时记录张数与点数和，引入标记变量：

$u$：记录取了多少张牌
$z$：记录点数之和

对每个点数 $j$，若它在多重集合中出现 $t$ 次，则贡献单项式 $(u\,y_j\,z^j)^t$。

点数 $j$ 可出现任意多次（包括 $0$ 次）的生成函数为几何级数：

\[\sum_{t=0}^{\infty}(u\,y_j\,z^j)^t = \frac{1}{1-u\,y_j\,z^j}\]

点数 $j$ 至少出现一次的生成函数为：

\[\sum_{t=1}^{\infty}(u\,y_j\,z^j)^t = \frac{u\,y_j\,z^j}{1-u\,y_j\,z^j}\]

$\Theta_k(c)$ 的定义

定义辅助生成函数

\[B_{c-1}(u,z):=\prod_{j=1}^{c-1}\frac{1}{1-u\,y_j\,z^j}\]

它枚举所有点数严格小于 $c$ 的牌的任意组合。

定义截断算子 $[z^{\le 13}]$，表示只保留 $z$ 的幂次不超过 $13$ 的项：

\[[z^{\le 13}]\Phi(z):=\sum_{s=0}^{13}[z^s]\Phi(z)\]

则按 $A_k=c$ 分层的前 $k$ 张牌的多重集合枚举多项式为

\[\Theta_k(c) := [z^{\le 13}]\,[u^k]\; \left(\frac{u\,y_c\,z^c}{1-u\,y_c\,z^c}\right) B_{c-1}(u,z)\]

解释：

$\dfrac{u\,y_c\,z^c}{1-u\,y_c\,z^c}$：点数 $c$ 至少出现一次（保证 $A_k=c$）
$B_{c-1}(u,z)$：点数 $1,\dots,c-1$ 各出现任意多次
$[u^k]$：恰好取 $k$ 张牌
$[z^{\le 13}]$：前 $k$ 张牌的点数和不超过 $13$

$K\ge k$ 的完整公式

剩余的 $4-k$ 张牌（即 $A_{k+1}, \dots, A_4$）必须满足 $\ge A_k = c$，即取自 ${c, c+1, \dots, 13}$。

因此，完整的多重集合枚举多项式为

\[U_{\ge k}(y) = \sum_{c=1}^{13}\Theta_k(c) \cdot \left(\sum_{d=c}^{13}y_d\right)^{4-k}\]

对应的有序四元组计数为

\[\#(K\ge k) = \Big(\mathrm{Lab}_4(U_{\ge k})\Big)\Big|_{y_1=\cdots=y_{13}=1}\]

代码及计算结果

代码：

  
"""
Compute #(K >= k) using generating functions directly.

Key formula:
Theta_k(c) = [z^{<=13}][u^k] * (u*y_c*z^c / (1-u*y_c*z^c)) * prod_{j=1}^{c-1} 1/(1-u*y_j*z^j)

The y_j variables track multiplicities, enabling:
1. Decoding of concrete multisets from coefficients
2. Direct computation of labeling coefficient Lab_n = n! / prod(m_j!)
"""

from collections import defaultdict, Counter
from math import factorial
from itertools import combinations_with_replacement


def multiply_poly(p1, p2, c, max_u, max_z):
    """
    Multiply two polynomials p1 * p2.

    Args:
        p1: First polynomial
        p2: Second polynomial
        c: Number of card values tracked in y_tuple
        max_u: Maximum u power to keep
        max_z: Maximum z power to keep

    Returns:
        Product polynomial as dict {(u_power, z_power, y_tuple): coefficient}

    Polynomial representation: {(u_power, z_power, y_tuple): coefficient}
    where y_tuple = (m_1, ..., m_c) records multiplicity of each card value.
    """
    result = defaultdict(int)
    for (u1, z1, y1), c1 in p1.items():
        for (u2, z2, y2), c2 in p2.items():
            u_new = u1 + u2
            z_new = z1 + z2
            if u_new <= max_u and z_new <= max_z:
                y_new = tuple(y1[i] + y2[i] for i in range(c))
                result[(u_new, z_new, y_new)] += c1 * c2
    return dict(result)


def at_least_one_geometric(j, c, max_u, max_z):
    """
    Compute u*y_j*z^j / (1 - u*y_j*z^j) truncated.

    Args:
        j: Card value
        c: Number of card values tracked in y_tuple
        max_u: Maximum u power to keep
        max_z: Maximum z power to keep

    Returns:
        Polynomial representing "at least one card with value j"
    """
    result = {}
    for t in range(1, max_u + 1):
        z_power = t * j
        if z_power <= max_z:
            y_tuple = tuple(t if idx == j - 1 else 0 for idx in range(c))
            result[(t, z_power, y_tuple)] = 1
    return result


def geometric_series(j, c, max_u, max_z):
    """
    Compute 1 / (1 - u*y_j*z^j) truncated.

    Args:
        j: Card value
        c: Number of card values tracked in y_tuple
        max_u: Maximum u power to keep
        max_z: Maximum z power to keep

    Returns:
        Polynomial representing "any number (including 0) of cards with value j"
    """
    result = {}
    for t in range(0, max_u + 1):
        z_power = t * j
        if z_power <= max_z:
            y_tuple = tuple(t if idx == j - 1 else 0 for idx in range(c))
            result[(t, z_power, y_tuple)] = 1
    return result


def compute_theta(c, k, max_z=13):
    """
    Compute Theta_k(c) using generating functions.

    Args:
        c: The value that A_k must equal
        k: Number of elements in the subset
        max_z: Maximum sum allowed (default 13)

    Returns:
        List of multisets (as sorted tuples) where A_k = c and sum <= max_z
    """
    max_u = k

    # Start with: at least one card with value c
    poly = at_least_one_geometric(c, c, max_u, max_z)

    # Multiply by 1/(1-u*y_j*z^j) for each j < c
    for j in range(1, c):
        factor = geometric_series(j, c, max_u, max_z)
        poly = multiply_poly(poly, factor, c, max_u, max_z)

    # Extract [u^k][z^{<=max_z}] and decode multisets from y-tuples
    multisets = []
    for (u_pow, z_pow, y_tuple), coef in poly.items():
        if u_pow == k and z_pow <= max_z:
            elements = []
            for j in range(c):
                elements.extend([j + 1] * y_tuple[j])
            elements.sort()
            multisets.append(tuple(elements))

    return sorted(multisets)


def labeling_coefficient(multiset, n):
    """
    Compute Lab_n = n! / prod(m_j!).

    Args:
        multiset: Tuple of card values
        n: Total number of cards

    Returns:
        Number of ways to arrange n cards with given multiset structure
    """
    counter = Counter(multiset)
    result = factorial(n)
    for m in counter.values():
        result //= factorial(m)
    return result


def compute_K_ge_k(k, n_cards=4, max_z=13):
    """
    Compute #(K >= k) for n_cards total cards.

    Args:
        k: Minimum subset size
        n_cards: Total number of cards (default 4)
        max_z: Maximum sum allowed (default 13)

    Returns:
        (total_count, details_by_c): Total count and breakdown by c value
    """
    total_count = 0
    details_by_c = {}
    remaining_cards = n_cards - k

    for c in range(1, 14):
        theta_multisets = compute_theta(c, k, max_z)

        if not theta_multisets:
            continue

        c_count = 0

        for first_k_multiset in theta_multisets:
            for extra in combinations_with_replacement(range(c, 14), remaining_cards):
                full_multiset = tuple(sorted(first_k_multiset + extra))
                lab = labeling_coefficient(full_multiset, n_cards)
                c_count += lab

        details_by_c[c] = {
            'theta_multisets': theta_multisets,
            'count': c_count
        }
        total_count += c_count

    return total_count, details_by_c


def print_detailed_results(k):
    """
    Print detailed breakdown for a specific k value.

    Args:
        k: The k value to analyze

    Returns:
        The computed result for #(K >= k)
    """
    result, details = compute_K_ge_k(k)

    print("=" * 70)
    print(f"K >= {k}  (A_1 + A_2 + ... + A_{k} <= 13)")
    print("=" * 70)

    print(f"\n[Breakdown by A_{k} = c]")
    print(f"{'c':<4} {'|Theta|':<8} {'Contribution':<14} {'Cumulative':<12} Theta_{k}(c)")
    print("-" * 70)

    cumsum = 0
    for c in sorted(details.keys()):
        cumsum += details[c]['count']
        theta_size = len(details[c]['theta_multisets'])
        multisets_str = str(details[c]['theta_multisets'])
        print(f"{c:<4} {theta_size:<8} {details[c]['count']:<14} {cumsum:<12} {multisets_str}")

    print(f"\n#(K >= {k}) = {result}")
    print(f"P(K >= {k}) = {result}/28561 = {result/28561:.6f}")

    return result


def print_summary():
    """Print summary table of all k values."""
    k2, _ = compute_K_ge_k(2)
    k3, _ = compute_K_ge_k(3)
    k4, _ = compute_K_ge_k(4)

    print("=" * 70)
    print("Summary")
    print("=" * 70)

    total = 13**4
    print(f"\n{'k':<5} {'#(K >= k)':<12} {'P(K >= k)':<12} {'#(K = k)':<12} {'P(K = k)':<12}")
    print("-" * 55)
    print(f"{1:<5} {total:<12} {total/total:<12.6f} {total - k2:<12} {(total-k2)/total:<12.6f}")
    print(f"{2:<5} {k2:<12} {k2/total:<12.6f} {k2 - k3:<12} {(k2-k3)/total:<12.6f}")
    print(f"{3:<5} {k3:<12} {k3/total:<12.6f} {k3 - k4:<12} {(k3-k4)/total:<12.6f}")
    print(f"{4:<5} {k4:<12} {k4/total:<12.6f} {k4:<12} {k4/total:<12.6f}")


if __name__ == "__main__":
    print("=" * 70)
    print("Computing #(K >= k) using Generating Functions")
    print("=" * 70)

    for k in [2, 3]:
        print()
        print_detailed_results(k)

    print()
    print_summary()

计算结果：

======================================================================
Computing #(K >= k) using Generating Functions
======================================================================

======================================================================
K >= 2  (A_1 + A_2 + ... + A_2 <= 13)
======================================================================

[Breakdown by A_2 = c]
c    |Theta|  Contribution   Cumulative   Theta_2(c)
----------------------------------------------------------------------
1    1        913            913          [(1, 1)]
2    2        2359           3272         [(1, 2), (2, 2)]
3    3        3289           6561         [(1, 3), (2, 3), (3, 3)]
4    4        3775           10336        [(1, 4), (2, 4), (3, 4), (4, 4)]
5    5        3889           14225        [(1, 5), (2, 5), (3, 5), (4, 5), (5, 5)]
6    6        3703           17928        [(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6)]
7    6        3048           20976        [(1, 7), (2, 7), (3, 7), (4, 7), (5, 7), (6, 7)]
8    5        1820           22796        [(1, 8), (2, 8), (3, 8), (4, 8), (5, 8)]
9    4        976            23772        [(1, 9), (2, 9), (3, 9), (4, 9)]
10   3        444            24216        [(1, 10), (2, 10), (3, 10)]
11   2        152            24368        [(1, 11), (2, 11)]
12   1        28             24396        [(1, 12)]

#(K >= 2) = 24396
P(K >= 2) = 24396/28561 = 0.854172

======================================================================
K >= 3  (A_1 + A_2 + ... + A_3 <= 13)
======================================================================

[Breakdown by A_3 = c]
c    |Theta|  Contribution   Cumulative   Theta_3(c)
----------------------------------------------------------------------
1    1        49             49           [(1, 1, 1)]
2    3        319            368          [(1, 1, 2), (1, 2, 2), (2, 2, 2)]
3    6        793            1161         [(1, 1, 3), (1, 2, 3), (1, 3, 3), (2, 2, 3), (2, 3, 3), (3, 3, 3)]
4    10       1399           2560         [(1, 1, 4), (1, 2, 4), (1, 3, 4), (1, 4, 4), (2, 2, 4), (2, 3, 4), (2, 4, 4), (3, 3, 4), (3, 4, 4), (4, 4, 4)]
5    13       1932           4492         [(1, 1, 5), (1, 2, 5), (1, 3, 5), (1, 4, 5), (1, 5, 5), (2, 2, 5), (2, 3, 5), (2, 4, 5), (2, 5, 5), (3, 3, 5), (3, 4, 5), (3, 5, 5), (4, 4, 5)]
6    12       1798           6290         [(1, 1, 6), (1, 2, 6), (1, 3, 6), (1, 4, 6), (1, 5, 6), (1, 6, 6), (2, 2, 6), (2, 3, 6), (2, 4, 6), (2, 5, 6), (3, 3, 6), (3, 4, 6)]
7    9        1170           7460         [(1, 1, 7), (1, 2, 7), (1, 3, 7), (1, 4, 7), (1, 5, 7), (2, 2, 7), (2, 3, 7), (2, 4, 7), (3, 3, 7)]
8    6        660            8120         [(1, 1, 8), (1, 2, 8), (1, 3, 8), (1, 4, 8), (2, 2, 8), (2, 3, 8)]
9    4        324            8444         [(1, 1, 9), (1, 2, 9), (1, 3, 9), (2, 2, 9)]
10   2        126            8570         [(1, 1, 10), (1, 2, 10)]
11   1        30             8600         [(1, 1, 11)]

#(K >= 3) = 8600
P(K >= 3) = 8600/28561 = 0.301110

======================================================================
Summary
======================================================================

k     #(K >= k)    P(K >= k)    #(K = k)     P(K = k)
-------------------------------------------------------
1     28561        1.000000     4165         0.145828
2     24396        0.854172     15796        0.553062
3     8600         0.301110     7885         0.276076
4     715          0.025034     715          0.025034

资援牌数期望问题

现在我们进一步研究：定义无法发动资援时交牌数为 0，求交牌数的无条件期望。

考虑两种策略：

最大化策略：在所有和为13的组合中，选择牌数最多的组合
最小化策略：在所有和为13的组合中，选择牌数最少的组合

例如，手牌为 ${1, 1, 11, 12, 13}$ 时，和为13的组合有：

${13}$（1张牌）
${1, 12}$（2张牌，有两种选法）
${1, 1, 11}$（3张牌）

最大化策略选择 ${1, 1, 11}$，交出3张牌；最小化策略选择 ${13}$，交出1张牌。

极值牌数问题：在 $n$ 张随机手牌的情况下，选择牌数极值（最大或最小）的和为13组合，交出牌数的数学期望是多少？

设 $X_1, X_2, \ldots, X_n$ 为独立同分布随机变量，$X_i \sim \mathrm{Unif}{1, 2, \ldots, 13}$。

定义可行子集族： $\mathcal{S}_n := \left\{I \subseteq \{1,\ldots,n\} : I \neq \varnothing,\ \sum_{i \in I} X_i = 13\right\}$

定义极值牌数： $M_n^{\max} := \begin{cases} \max_{I \in \mathcal{S}_n} |I| & \text{if } \mathcal{S}_n \neq \varnothing \\ 0 & \text{otherwise} \end{cases}$

\[M_n^{\min} := \begin{cases} \min_{I \in \mathcal{S}_n} |I| & \text{if } \mathcal{S}_n \neq \varnothing \\ 0 & \text{otherwise} \end{cases}\]

目标：计算 $\mathbb{E}[M_n^{\max}]$ 和 $\mathbb{E}[M_n^{\min}]$。

状态定义

与原问题类似，我们用动态规划追踪可达子集和的信息。但这里需要记录的不是”是否可达”，而是”达到该和的极值牌数”。

状态：$\mathbf{d} = (d_0, d_1, \ldots, d_{13})$

对于最大化问题：$d_k$ 表示达到子集和 $k$ 所能使用的最大牌数，$-1$ 表示不可达
对于最小化问题：$d_k$ 表示达到子集和 $k$ 所需的最小牌数，$\infty$ 表示不可达

状态转移（加入一张值为 $x$ 的新牌）：

最大化：$d'_k = \max(d_k, d_{k-x} + 1)$
最小化：$d'_k = \min(d_k, d_{k-x} + 1)$

关键性质：状态空间是有限的！

对于最大化：$d_k \in {-1, 0, 1, \ldots, k}$，因为和为 $k$ 最多用 $k$ 张点数为1的牌
对于最小化：$d_k \in {1, 2, \ldots, k, \infty}$，同理

因此，这仍然是有限状态时齐马尔可夫链，存在封闭形式。

代码及计算结果

在原代码基础上进行最小改动。核心变化是：将二进制掩码替换为记录极值牌数的元组（tuple）。该元组的状态是 $\mathbf d=(d_0,\dots,d_T)$，用字典计数，实际遍历的是可达状态集合$\Omega_T := {\mathbf d \text{ 在转移闭包下可达}}$。

  
from collections import defaultdict
from math import gcd


def extremal_cards_probability(n, target=13, max_value=13, mode='max'):
    """
    Computes the expected number of cards when choosing the subset
    with extremal (max or min) cardinality that sums to `target`.

    Args:
        n: Number of cards in hand
        target: Target sum (default 13)
        max_value: Maximum card value (default 13)
        mode: 'max' for maximum cardinality, 'min' for minimum cardinality

    Returns:
        (numerator, denominator): Reduced fraction of expected value

    Core idea:
    - Track the extremal (max or min) number of cards needed to reach each sum.
    - Use dynamic programming over states, where each state records
      the best cardinality to achieve each possible sum from 0 to target.
    """

    WIDTH = target + 1

    # Mode-specific configuration
    # For 'max': find largest subset, UNREACHABLE = -1
    # For 'min': find smallest subset, UNREACHABLE = n+1
    if mode == 'max':
        UNREACHABLE = -1
        initial_state = tuple([0] + [UNREACHABLE] * target)

        def update(old_val, new_val):
            if old_val == UNREACHABLE:
                return new_val
            return max(old_val, new_val)

        def is_reachable(val):
            return val >= 0
    else:  # mode == 'min'
        UNREACHABLE = n + 1
        initial_state = tuple([0] + [UNREACHABLE] * target)

        def update(old_val, new_val):
            return min(old_val, new_val)

        def is_reachable(val):
            return val <= n

    # DP state: tuple where state[k] = extremal card count to reach sum k
    # dp[state] = count of sequences producing this state
    dp = defaultdict(int)
    dp[initial_state] = 1

    # Main DP loop: add one card at a time
    for _ in range(n):
        new_dp = defaultdict(int)

        for state, count in dp.items():
            for x in range(1, max_value + 1):
                new_state = list(state)

                # Update high to low to avoid reusing the same card
                for k in range(target, x - 1, -1):
                    if is_reachable(state[k - x]):
                        new_state[k] = update(new_state[k], state[k - x] + 1)

                new_dp[tuple(new_state)] += count

        dp = new_dp

    # Compute expected value: sum of (cardinality × count) for reachable states
    numerator = sum(
        state[target] * count
        for state, count in dp.items()
        if is_reachable(state[target])
    )

    denominator = max_value ** n

    g = gcd(numerator, denominator)
    return numerator // g, denominator // g

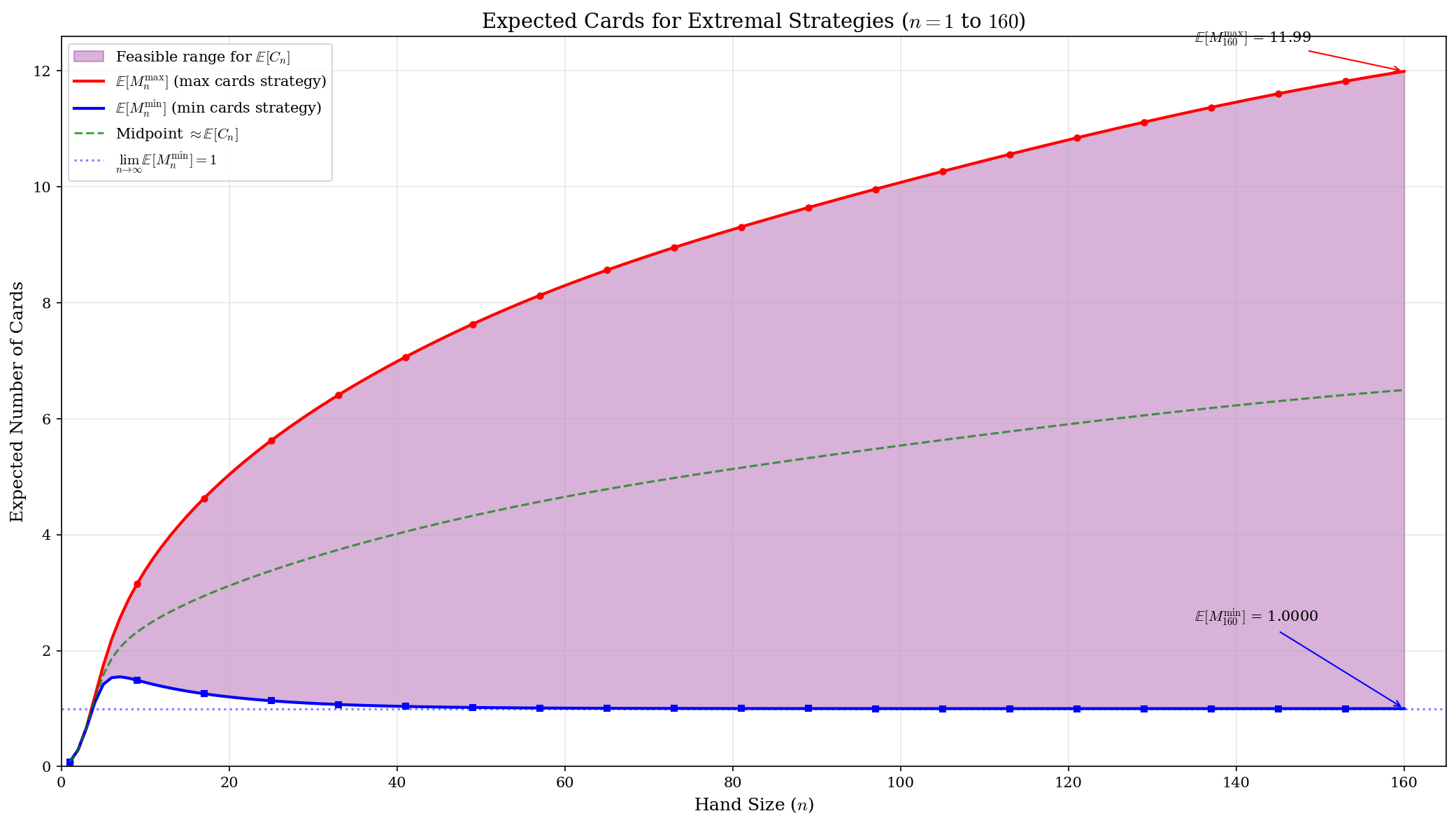
计算结果（选取一些典型的$n$值为例）：

$n$	$\mathbb{E}[M_n^{\min}]$	$\mathbb{E}[M_n^{\max}]$	区间宽度
1	$\frac{1}{13} \approx 0.077$	$\frac{1}{13} \approx 0.077$	$0$
2	$\frac{49}{169} \approx 0.290$	$\frac{49}{169} \approx 0.290$	$0$
3	$0.664$	$0.680$	$0.016$
4	$1.109$	$1.210$	$0.102$
5	$1.418$	$1.744$	$0.326$
6	$1.533$	$2.194$	$0.661$
7	$1.549$	$2.565$	$1.016$
8	$1.526$	$2.877$	$1.351$
9	$1.490$	$3.147$	$1.657$
10	$1.453$	$3.386$	$1.933$
40	1.0407	6.99	5.95
80	1.0017	9.26	8.26
120	1.000067	10.81	9.81
160	1.000003	11.99	10.99

根据以上计算结果及图像，我们可以得出以下结论：

【最大化策略】

$\mathbb{E}[M_n^{\max}]$：随 $n$ 单调递增，渐近线性增长。手牌越多，越可能找到牌数更多的组合。

命题

\[\mathbb E[M_{n+1}^{\max}] \ge \mathbb E[M_n^{\max}]\]

证明

对任意确定的手牌序列 $(x_1,\ldots,x_n)$ 以及任意 $x_{n+1}\in{1,\ldots,13}$，都有逐点不等式

\[M_{n+1}^{\max}(x_1,\ldots,x_n,x_{n+1}) \ge M_n^{\max}(x_1,\ldots,x_n)\]

其原因在于：在 $n+1$ 张牌的问题中，可以选择不使用第 $n+1$ 张牌，因此 $n$ 张牌问题中的最优解对应的子集仍然是一个可行解。

由于期望保持逐点不等式，上式对随机变量取期望即可得到

\[\mathbb E[M_{n+1}^{\max}] \ge \mathbb E[M_n^{\max}] \tag*{$\square$}\]

【最小化策略】

$\mathbb{E}[M_n^{\min}]$：数值上呈单峰：先增后减，并趋于$1$。趋于$1$的原因是$n$足够大时几乎必然抽到$13$，使得最小可行子集为单张。

命题1

\[\lim_{n\to\infty}\mathbb E[M_n^{\min}] = 1\]

证明

令事件

\[A_n=\{\text{手牌中至少出现一张点数为 }13\}\]

则

\[\mathbb P(A_n)=1-\left(\frac{12}{13}\right)^n\]

当事件 $A_n$ 发生时，单张点数为 $13$ 的牌即可构成一个子集和为 $13$ 的可行解，因此

\[M_n^{\min}=1\]

当事件 $A_n^c$ 发生时，未必存在子集和为 $13$ 的可行解；在本文的约定下，此时 $M_n^{\min}$ 取值为 $0$。无论是否存在可行解，随机变量 $M_n^{\min}$ 都满足一致有界性

\[0 \le M_n^{\min} \le 13\]

因此对所有样本点均成立逐点不等式

\[\mathbf 1_{A_n} \le M_n^{\min} \le \mathbf 1_{A_n}+13\,\mathbf 1_{A_n^c}\]

对上式取期望，得到夹逼关系

\[\mathbb P(A_n) \le \mathbb E[M_n^{\min}] \le \mathbb P(A_n)+13\,\mathbb P(A_n^c)\]

代入 $\mathbb P(A_n^c)=\left(\frac{12}{13}\right)^n$，可得

\[1-\left(\frac{12}{13}\right)^n \le \mathbb E[M_n^{\min}] \le 1+12\left(\frac{12}{13}\right)^n\]

令 $n\to\infty$，两端同趋于 $1$，由夹逼定理得到

\[\lim_{n\to\infty}\mathbb E[M_n^{\min}] = 1 \tag*{$\square$}\]

命题2

令 $M_n=M_n^{\min}$，并约定若无法凑出 $13$ 则取 $M_n=0$。则序列 $\mathbb E[M_n]$ 是单峰的。更具体地，存在某个 $n^*$ 使得

\[\mathbb E[M_1]\le\cdots\le \mathbb E[M_{n^{*}}]\ge \mathbb E[M_{n^{*}+1}]\ge\cdots\]

并且在本文参数下峰值出现在 $n^*=7$

证明

记事件

\[E_n=\{\text{前 }n\text{ 张牌存在子集和为 }13\}\]

以及

\[A_n=\{\text{前 }n\text{ 张牌至少出现一张 }13\}\]

显然 $A_n\subseteq E_n$

设

\[\Delta_n=\mathbb E[M_{n+1}]-\mathbb E[M_n]\]

将差分分解为

\[\Delta_n=\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n}]+\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n^c}]\]

首先，在 $E_n$ 发生时，前 $n$ 张牌已经存在一个可行解。加入第 $n+1$ 张牌后仍可选择不使用新牌，因此最小可行张数不会增大，即

\[M_{n+1}\le M_n\]

从而

\[\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n}]\le 0\]

其次，在 $E_n^c$ 上按约定 $M_n=0$，并且恒有 $0\le M_{n+1}\le 13$，因此

\[0\le (M_{n+1}-M_n)\mathbf 1_{E_n^c}=M_{n+1}\mathbf 1_{E_n^c}\le 13\mathbf 1_{E_n^c}\]

从而

\[\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n^c}]\le 13\mathbb P(E_n^c)\]

另一方面，考虑事件 $E_n\cap A_n^c\cap{X_{n+1}=13}$。在 $E_n\cap A_n^c$ 上，前 $n$ 张牌可凑出 $13$ 但不含 $13$，因此任何可行解至少需要两张牌，从而 $M_n\ge 2$。若再抽到 $X_{n+1}=13$，则单张 $13$ 立即给出大小为 1 的可行解，因此 $M_{n+1}=1$。于是该事件上有

\[M_{n+1}-M_n\le -1\]

而事件 $E_n$ 其余部分不为正，所以

\[\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n}] \le -\mathbb P(E_n\cap A_n^c\cap\{X_{n+1}=13\})\]

由于 $X_{n+1}$ 与前 $n$ 张独立且 $\mathbb P(X_{n+1}=13)=1/13$，有

\[\mathbb P(E_n\cap A_n^c\cap\{X_{n+1}=13\}) =\frac{1}{13}\mathbb P(E_n\cap A_n^c)\]

并且由 $A_n\subseteq E_n$ 得

\[\mathbb P(E_n\cap A_n^c)=\mathbb P(A_n^c)-\mathbb P(E_n^c)\]

因此

\[\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n}] \le -\frac{1}{13}\mathbb P(A_n^c)+\frac{1}{13}\mathbb P(E_n^c)\]

综合以上估计得到

\[\Delta_n\le -\frac{1}{13}\mathbb P(A_n^c)+\frac{170}{13}\mathbb P(E_n^c)\]

其中 $\frac{170}{13}$ 来自对 $\mathbb E[(M_{n+1}-M_n)\mathbf 1_{E_n^c}]$ 的系数合并

下面估计两项概率。首先

\[\mathbb P(A_n^c)=\left(\frac{12}{13}\right)^n\]

其次，对 $\mathbb P(E_n^c)$ 给出一个粗上界。将互补点数组成 6 对

\[\{1,12\},\{2,11\},\{3,10\},\{4,9\},\{5,8\},\{6,7\}\]

若手牌中同时出现某一对互补点数，则两张牌即可凑出 $13$，因此 $E_n$ 发生。于是 $E_n^c$ 蕴含：不出现 $13$，且对每一对互补点数至少有一个点数完全缺失。对每对互补点数选择一个缺失者，共有 $2^6=64$ 种选择方案。固定一种方案后，所有牌必须落在某个至多含 $6$ 个点数的集合中，从而

\[\mathbb P(E_n^c)\le 64\left(\frac{6}{13}\right)^n\]

代入得到

\[\Delta_n \le -\frac{1}{13}\left(\frac{12}{13}\right)^n+\frac{170}{13}\cdot 64\left(\frac{6}{13}\right)^n\]

提取公共因子 $\frac{1}{13}\left(\frac{6}{13}\right)^n$ 可得

\[\Delta_n\le \frac{1}{13}\left(\frac{6}{13}\right)^n\Bigl(-2^n+10880\Bigr)\]

由于 $2^{14}=16384>10880$，从而对所有 $n\ge 14$ 有 $\Delta_n<0$，即

\[\mathbb E[M_{n+1}]<\mathbb E[M_n]\]

对所有 $n\ge 14$ 成立。

因此序列在尾部 $n\ge 14$ 时严格递减。另一方面，本文已用 DP 精确计算了 $1\le n\le 10$ 的 $\mathbb E[M_n]$，并验证它在该范围内先递增后递减，且峰值出现在 $n=7$。由于峰值点 $7$ 位于 $[1,10]$ 之内，并且在 $n\ge 14$ 时序列严格递减，故其后不可能再出现第二个峰值点。于是 $\mathbb E[M_n]$ 在全体 $n\ge 1$ 上单峰，且唯一峰值为 $n^*=7$。$\square$

由于状态空间有限且与 $n$ 无关，这两个问题都满足有限阶线性递推关系，生成函数是有理函数。

均匀随机选择组合

如果我们不总是选择极值组合，而是在所有可行组合中均匀随机选择一个，期望交出多少张牌？

例如，手牌 ${1, 1, 12, 13}$ 时，可行组合有：

${1, 12}$（用第一个1）：2张
${1, 12}$（用第二个1）：2张
${13}$：1张

均匀随机选择，期望牌数为 $\frac{2 + 2 + 1}{3} = \frac{5}{3}$。

定义 $N_n := \lvert \mathcal{S}_n \rvert$ 为和为13的子集个数，$T_n := \sum_{I \in \mathcal{S}_n}\lvert I\rvert$ 为这些子集的总牌数。

若 $N_n > 0$，从 $\mathcal{S}_n$ 中均匀随机选取 $I^*$，则

\[C_n := |I^*|\]

目标：计算 $\mathbb{E}[C_n] = \mathbb{E}\left[\frac{T_n}{N_n} \cdot \mathbf{1}_{N_n > 0}\right]$

要计算 $\mathbb{E}[T_n / N_n]$，我们需要追踪 $(N_n, T_n)$ 的联合分布，即对每个和 $k$，记录：

$c_k$：和为 $k$ 的子集个数
$t_k$：这些子集的总牌数

状态表示为 $((c_0, t_0), (c_1, t_1), \ldots, (c_{13}, t_{13}))$。

$c_k$ 的取值范围是 ${0, 1, \ldots, 2^n}$，随 $n$ 指数增长。这意味着状态空间大小不再有限，不能用动态规划方法。

由于状态空间无限，这不是有限状态马尔可夫链，因此不保证存在有限阶线性递推或有理生成函数，所以不太可能有简单的封闭形式

用极值问题界定均匀随机问题

尽管此问题难以精确求解，但我们可以利用极值问题给出上下界。

设在事件 $E_n={\mathcal S_n\neq\varnothing}$ 上，从所有满足子集和为 13 的子集中等概率随机选择一个，并记其所用牌数为随机变量 $C_n$。

显然有逐点不等式

\[M_n^{\min} \;\le\; C_n \;\le\; M_n^{\max},\]

根据期望的单调性，以下关系成立：

\[\mathbb E[M_n^{\min}] \;\le\; \mathbb E[C_n] \;\le\; \mathbb E[M_n^{\max}].\]

进一步地，数值计算显示，在若干中等规模的 $n$（例如 $n=5,8,10$）下，$\mathbb E[C_n]$ 与区间中点

\[\frac{1}{2}\bigl(\mathbb E[M_n^{\min}]+\mathbb E[M_n^{\max}]\bigr)\]

非常接近，误差相对较小。所以极值问题提供了研究均匀随机问题的有效工具：通过计算简单的上下界，我们可以在不穷举所有组合的情况下，得到复杂问题的精确范围和良好近似。

$n$	$\mathbb{E}[M_n^{\min}]$	$\mathbb{E}[C_n]$	$\mathbb{E}[M_n^{\max}]$	相对位置
5	$1.418$	$1.582$	$1.744$	$50.2\%$
8	$1.526$	$2.219$	$2.877$	$51.3\%$
10	$1.453$	$2.454$	$3.386$	$51.8\%$

需要强调的是，这一现象目前仅是经验性的数值观察。均匀随机选择可行子集所诱导的牌数分布，取决于不同大小子集在 $\mathcal S_n$ 中的数量分布，该分布并无显然的对称性保证。

总结

问题	状态数	时间复杂度	空间复杂度	封闭形式	方法
原问题（概率）	$\mathcal{O}(2^{T+1})$	$\mathcal{O}(n \cdot 2^{T+1} \cdot m)$	$\mathcal{O}(2^{T+1})$	存在	Bitmask DP
极值问题	$\mathcal{O}(2^{T+1})$	$\mathcal{O}(n\cdot \lvert \Omega_T \rvert \cdot m\cdot T)$	$\mathcal{O}( \lvert \Omega_T \rvert )$	存在	极值追踪 DP
均匀随机	$\mathcal{O}\left(\binom{n+T}{T}\right)$	$\mathcal{O}\left(\binom{n+T}{T} \cdot n \cdot m \cdot T\right)$	$\mathcal{O}\left(\binom{n+T}{T} \cdot T\right)$	不太可能	夹逼近似

其中 $T=13$（目标和），$m=13$（牌值范围）。

脚注

实际上，卡牌的点数并非均匀分布。点数【2】和【Q】的概率为$7/80$，而其它的点数概率为$3/40$。由于这种差异对计算结果的影响可以忽略不记，我们还是认为所有卡牌点数是均匀分布的。 ↩︎

math

sgs

This post is licensed under CC BY 4.0 by the author.

前言

研究范围

卡牌

数学模型

理想模型

现实模型

武将

武将技能概率

伯努利试验

邓艾（神话再临·山）

甄姬（标准版）

孟获（神话再临·林）

伯努利试验概率分布小结

黄月英（标准版）

袁绍（神话再临·火）

二次函数

王朗（SP）

生日问题

孙资&刘放（原创之魂2016）

周泰（神话再临·风）

神吕蒙（神话再临·风）

袁绍（神话再临·火）

和约束下可选子集最大规模的期望

曹冲（新一将成名2013）

随机子集和的可达性概率

糜竺（SP）

技能比较

额外摸牌

受到伤害后摸牌

总结

附录

称象获得牌数的组合生成函数解法

多重集合的单项式表示

升标号算子

从多重集合到有序四元组的计数

构造 $K\ge k$ 的多重集合枚举多项式

代码及计算结果

资援牌数期望问题

状态定义

代码及计算结果

均匀随机选择组合

总结

脚注

Trending Tags