Scheduling

Greedy

Minimum Swaps to Make Strings Equal

public int minimumSwap(String s1, String s2) {
    int[] count = new int[2];
    for (int i = 0; i < s1.length(); i++) {
        // ignores matched positions
        if (s1.charAt(i) != s2.charAt(i)) {
            count[s1.charAt(i) - 'x']++;
        }
    }

    // case 3: "x" "y"
    if ((count[0] + count[1]) % 2 == 1) {
        return -1;
    }

    // count[0] % 2 == count[1] % 2
    // case1: "xx" "yy" - 1 swap, apply as much as possible
    // case2: "xy" "yx" - 2 swaps
    return count[0] / 2 + count[1] / 2 + count[0] % 2 * 2;
}

Longest Happy String

public String longestDiverseString(int a, int b, int c) {
    return helper(a, b, c, "a", "b", "c");
}

private String helper(int a, int b, int c, String sa, String sb, String sc) {
    // preprocess, so that a >= b >= c
    if (a < b) {
        return helper(b, a, c, sb, sa, sc);
    }

    if (b < c) {
        return helper(a, c, b, sa, sc, sb);
    }

    if (b == 0) {
        return sa.repeat(Math.min(a, 2));
    }

    // greedy
    int aUsed = Math.min(a, 2), bUsed = a - aUsed >= b ? 1 : 0; 
    return sa.repeat(aUsed) + sb.repeat(bUsed) + helper(a - aUsed, b - bUsed, c, sa, sb, sc);
}

String Without AAA or BBB

Task Scheduler

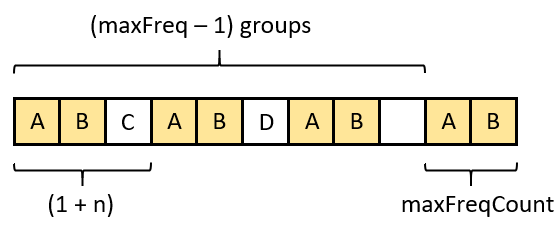
int leastInterval(vector<char>& tasks, int n) {
    vector<int> freqs(26);
    int maxFreq = 0, maxFreqCount = 0;  // Count of the most frequent tasks
    for (const char& ch : tasks) {
        freqs[ch - 'A']++;
        if (maxFreq == freqs[ch - 'A']) {
            maxFreqCount++;
        } else if (maxFreq < freqs[ch - 'A']) {
            maxFreq = freqs[ch - 'A'];
            maxFreqCount = 1;
        }
    }

    // No idle vs has idle
    return max(static_cast<int>(tasks.size()), (maxFreq - 1) * (n + 1) + maxFreqCount);
}

Maximum Number of Weeks for Which You Can Work

public long numberOfWeeks(int[] milestones) {
    long sum = 0;
    int max = 0;
    for (int m : milestones) {
        sum += m;
        max = Math.max(max, m);
    }

    // Case 1: there are more than one max.
    // takes turns working on projects that have max milestones
    // e.g. [4, 4, 2, 1]
    // -> [3, 3, 2, 1] +2
    // -> [2, 2, 2, 1] +2
    // -> [1, 1, 1, 1] +3
    // -> [0, 0, 0, 0] +4

    // Case 2: there is only one max
    // strategy:
    // - max: a0, second: a1, remaining projects: r
    // 1. works on a0 and any one from r, until a0 is reduced to a1
    // 2. then we have two max projects (a1) - back to Case 1
    //
    // for Step 1, it's required sum(r) >= a0 - a1
    // -> sum(r) + a1 - a0 >= 0
    // -> sum - 2 * max >= 0

    // Case 3: the requirement in Step 1, Case 2 is not met
    // stragy:
    // max -> any one from others -> max -> ...
    // e.g. [3, 1]
    // -> [2, 0] +2
    // -> [1, 0] +1
    return (sum - max) < max ? 2 * (sum - max) + 1 : sum;
}

EDF

Earliest deadline first scheduling

Rearrange String k Distance Apart

public String rearrangeString(String s, int k) {
    if (k == 0) {
        return s;
    }

    int[] count = new int[26];
    for (char c : s.toCharArray()) {
        count[c - 'a']++;
    }

    Queue<Integer> pq = new PriorityQueue<>(Comparator.comparingInt(i -> -count[i]));
    for (int i = 0; i < 26; i++) {
        if (count[i] > 0) {
            pq.offer(i);
        }
    }

    StringBuilder sb = new StringBuilder();
    Queue<Integer> q = new LinkedList<>();
    while (!pq.isEmpty()) {
        // picks the char with highest frequency
        int node = pq.poll();
        sb.append((char)(node + 'a'));
        count[node]--;

        // adds used char to the queue
        q.offer(node);

        // maintains fixed size k
        if (q.size() == k) {
            // front char is already at least k char apart
            int front = q.poll();
            if (count[front] > 0) {
                pq.offer(front);
            }
        }
    }
    return sb.length() == s.length() ? sb.toString() : "";
}

NP-Complete

Parallel Courses II

// NP-complete
// O(3 ^ n)
public int minNumberOfSemesters(int n, int[][] dependencies, int k) {
    // bit mask of prerequisite courses
    int[] p = new int[n];
    for (int[] d : dependencies) {
        p[d[1] - 1] |= 1 << (d[0] - 1);
    }

    int[] dp = new int[1 << n];
    Arrays.fill(dp, n);
    dp[0] = 0;

    // state represents the courses that have been taken so far
    for (int state = 0; state < (1 << n); state++) {
        int courses = 0;
        for (int i = 0; i < n; i++) {
            // prerequisite courses of i is a subset of current state
            // so we can take course i
            if ((state & p[i]) == p[i]) {
                courses |= (1 << i);
            }
        }

        // removes courses that have been taken
        courses &= ~state;

        // enumerates all subsets of courses
        for (int s = courses; s > 0; s = (s - 1) & courses) {
            if (Integer.bitCount(s) <= k) {
                // state | s is the next state after taking the courses in s
                dp[state | s] = Math.min(dp[state | s], dp[state] + 1);
            }
        }
    }
    return dp[(1 << n) - 1];
}