Reverse Thinking

Maximum Segment Sum After Removals

private long[] parents;

public long[] maximumSegmentSum(int[] nums, int[] removeQueries) {
    // reverse union-find
    int n = nums.length;
    this.parents = new long[n];
    // max long is used to mark unvisited
    Arrays.fill(parents, Long.MAX_VALUE);

    long[] answer = new long[n];
    for (int i = n - 1; i > 0; i--) {
        int q = removeQueries[i];
        parents[q] = -nums[q];

        // unions with left interval
        if (q > 0 && parents[q - 1] != Long.MAX_VALUE) {
            union(q, q - 1);
        }

        // unions with right interval
        if (q < n - 1 && parents[q + 1] != Long.MAX_VALUE) {
            union(q, q + 1);
        }

        answer[i - 1] = Math.max(answer[i], -parents[find(q)]);
    }
    return answer;
}

private int find(int u) {
    return parents[u] < 0 ? u : (int)(parents[u] = find((int)parents[u]));
}

private void union(int u, int v) {
    int pu = find(u), pv = find(v);
    // negated sum
    parents[pv] += parents[pu];
    parents[pu] = pv;
}

This problem can also be resolved by TreeMap of intervals.

Execution of All Suffix Instructions Staying in a Grid

// notice the direction is opposition to the instruction
// because we will process the instructions in reverse order
private static final Map<Character, int[]> DIRECTIONS = Map.of(
    'U', new int[]{1, 0},
    'L', new int[]{0, 1},
    'D', new int[]{-1, 0},
    'R', new int[]{0, -1}
);

public int[] executeInstructions(int n, int[] startPos, String s) {
    // offset[i]: steps to move off the grid from the start position in the i-th direction
    // {top, left, bottom, right}
    //
    // assume the grid has no boundary
    int[] offsets = {startPos[0] + 1, startPos[1] + 1, startPos[0] - n, startPos[1] - n};

    int m = s.length();
    // maps[i]: {pos[i], last seen instruction index when robot is at pos[i]}
    Map<Integer, Integer>[] maps = new Map[2];
    maps[0] = new HashMap<>();  // horizontal
    maps[1] = new HashMap<>();  // vertical
    maps[0].put(0, m);
    maps[1].put(0, m);

    // virtualPos[i]: the virtual location that if the robot starts here at the i-th instruction
    //    finally it will reach (0, 0) following the remaining instruction sequence
    //
    // assume the robot starts from the i-th instruction and ends at the top border (-1) at a certain instruction
    // at the i-th time, the mirror robot is at (pos[0], pos[1])
    // now we are computing which row is the end row of virtual robot
    // denote the end position of mirror as (virtualEnd[0], virtualEnd[1])
    // in the vertical direction, we have:
    //  startPos[0] - (-1) = virtualPos[0] - virtualEnd[0]
    //  virtualEnd[0] = virtualPos[0] - (startPos[0] + 1)
    //    = virtualPos[0] - offset[top]
    //
    // now we processes the instructions in reverse order
    int[] virtualPos = new int[2], answer = new int[m];
    for (int i = m - 1; i >= 0; i--) {
        int[] instr = DIRECTIONS.get(s.charAt(i));
        virtualPos[0] += instr[0];
        virtualPos[1] += instr[1];

        int min = m - i;
        for (int j = 0; j < offsets.length; j++) {
            // 2 * m - (i + 1) >= m, so we use it as the default value
            // if there was an instruction with index j when virtualPos equals this threshold (virtualPos - offset)
            // then the real robot will be at border at index j
            // so the feasible instructions are (j - i - 1)
            min = Math.min(min, maps[j % 2].getOrDefault(virtualPos[j % 2] - offsets[j], 2 * m) - i - 1);
        }

        maps[0].put(virtualPos[0], i);
        maps[1].put(virtualPos[1], i);
        answer[i] = min;
    }
    return answer;
}

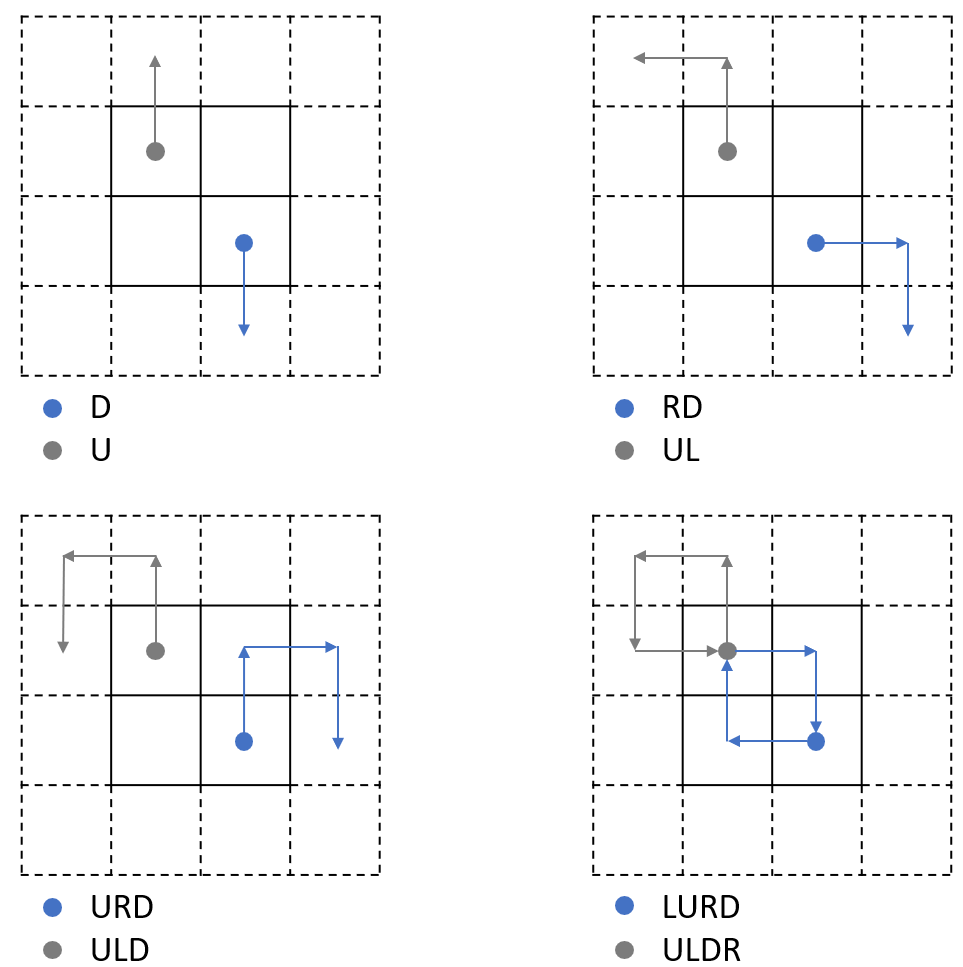
For example, n = 2, startPos = [1,1], s = "LURD"

We can see at each instruction, the virtual robot will eventually reach (0, 0) following the remaining instruction sequence.

Sum of Matrix After Queries