Random

Shuffle

Fisher-Yates shuffle

Shuffle an Array

private int[] arr;
private int[] oldArr;

private Random rand = new Random();

public Solution(int[] nums) {
    arr = nums;
    oldArr = nums.clone();
}

/** Resets the array to its original configuration and return it. */
public int[] reset() {
    return oldArr;
}

/** Returns a random shuffling of the array. */
public int[] shuffle() {
    for (int i = 0; i < arr.length; i++) {
        swap(i, i + rand.nextInt(arr.length - i));
    }
    return arr;
}

private void swap(int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

Random Flip Matrix

private Map<Integer, Integer> map;  // index : real index
private Random rand;
private int rows, cols, count;

public Solution(int n_rows, int n_cols) {
    map = new HashMap<>();
    rand = new Random();
    rows = n_rows;
    cols = n_cols;
    reset();
}

public int[] flip() {
    int index = rand.nextInt(count--);

    // swaps the real index at index and count
    int tmp = map.getOrDefault(index, index);        
    map.put(index, map.getOrDefault(count, count));
    map.put(count, tmp);

    return new int[]{tmp / cols, tmp % cols};
}

public void reset() {
    // no need to clear the map
    count = rows * cols;
}

Remapping

Insert Delete GetRandom O(1)

Map + List

Random Pick with Blacklist

private Map<Integer, Integer> map = new HashMap<>();
private Random rand = new Random();
private int whitelistSize;  // number of integers in whitelist

public Solution(int n, int[] blacklist) {
    whitelistSize = n - blacklist.length;

    // some blacklist integers already occupies positions in [whitelistSize, n)
    for (int b : blacklist) {
        if (b >= whitelistSize) {
            map.put(b, -1);
        }  
    }

    // re-maps blacklist integers to the segment [whitelistSize, n)
    int index = n - 1;
    for (int b : blacklist) {
        // finds the first vacant position in [whitelistSize, n)
        // and maps b to it
        if (b < whitelistSize) {
            while (map.containsKey(index--)) {
            }
            map.put(b, index + 1);
        }
    }
}

public int pick() {
    int num = rand.nextInt(whitelistSize);
    return map.getOrDefault(num, num);
}

The above problem can be solved by binary search, too. But the time complexity will be higher:

private int[] blacklist;
private Random rand = new Random();
private int whitelistSize;  // number of integers in whitelist

public Solution(int n, int[] blacklist) {
    this.blacklist = blacklist;
    this.whitelistSize = n - blacklist.length;

    Arrays.sort(blacklist);
}

// O(log(n))
public int pick() {
    int num = rand.nextInt(whitelistSize);
    // if num is in [0, blacklist[0]), returns num
    // if num is in [blacklist[0], blacklist[1] - 1), returns num + 1
    // ...
    // if num is in [blacklist[i] - i, blacklist[i + 1] - (i + 1)), returns num + (i + 1)
    // ...
    // searches for the index of the first right boundary so that blacklist[index] - index > num
    // i.e. blacklist[index] - index - 1 >= num
    int low = 0, high = blacklist.length;
    while (low < high) {
        int mid = (low + high) >>> 1;
        if (blacklist[mid] - mid - 1 >= num) {
            high = mid;
        } else {
            low = mid + 1;
        }
    }
    return num + low;
}

Cumulative Probability

Random Pick with Weight

private int[] p;  // cumulative sum
private Random rand = new Random();

public Solution(int[] w) {
    p = new int[w.length + 1];
    for (int i = 0; i < w.length; i++) {
        p[i + 1] = p[i] + w[i];
    }
}

public int pickIndex() {
    // target range: [1, sum]
    int index = Arrays.binarySearch(p, rand.nextInt(p[p.length - 1]) + 1);
    // w starts from p[1], therefore index - 1
    return (index < 0 ? ~index : index) - 1;
}

Multi-dimension

Random Point in Non-overlapping Rectangles

private int[][] rects;
private int[] p;
private Random rand = new Random();

public Solution(int[][] rects) {
    this.rects = rects;

    p = new int[rects.length + 1];
    for (int i = 0; i < rects.length; i++) {
        // number of points
        p[i + 1] = p[i] + (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);
    }
}

public int[] pick() {
    int points = rand.nextInt(p[p.length - 1]) + 1;
    int i = Arrays.binarySearch(p, points);
    int index = i < 0 ? ~i : i;

    // rect starts from p[1], therefore index - 1
    int[] rect = rects[index - 1];
    int left = rect[0], bottom = rect[1], right = rect[2], top = rect[3];
    int x = left + (p[index] - points) % (right - left + 1);
    int y = bottom + (p[index] - points) / (right - left + 1);
    return new int[]{x, y};
}

Sampling

Rejection Sampling

Rejection sampling: acceptance-rejection method

The algorithm to obtain a sample from distribution \(X\) with density \(f\) using samples from distribution \(Y\) with density \(g\) is as follows:

• Obtain a sample \(y\) from distribution \(Y\) and a sample \(u\) from \(\mathrm {Unif} (0,1)\) (the uniform distribution over the unit interval).
• Check whether or not \(u<f(y)/Mg(y)\).
  • If this holds, accept \(y\) as a sample drawn from \(f\);
  • if not, reject the value of \(y\) and return to the sampling step.

The algorithm will take an average of \(M\) iterations to obtain a sample.

(from https://theclevermachine.files.wordpress.com/2012/09/rejectionsamplingcriterion.png?w=584)

Implement Rand10() Using Rand7()

(from https://leetcode.com/problems/implement-rand10-using-rand7/Figures/470/rejectionSamplingTable.png)

public int rand10() {
    int row, col, index;
    do {
        row = rand7();
        col = rand7();
        index = col + (row - 1) * 7;
    } while (index > 40);
    return 1 + index % 10;
}

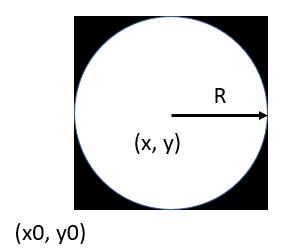
Generate Random Point in a Circle

private double r, x, y;

public Solution(double radius, double x_center, double y_center) {
    this.r = radius;
    this.x = x_center;
    this.y = y_center;
}

public double[] randPoint() {
    double x0 = x - r;
    double y0 = y - r;

    while (true) {
        double xr = x0 + Math.random() * r * 2;
        double yr = y0 + Math.random() * r * 2;
        if ((xr - x) * (xr - x) + (yr - y) * (yr - y) <= r * r) {
            return new double[]{xr, yr};
        }
    }
}

Inverse Transform Sampling

Inverse transform sampling

1. Generate a random number \(u\) from the standard uniform distribution in the interval \([0,1]\), e.g. from \(U\sim \mathrm {Unif} [0,1]\)
2. Find the inverse of the desired CDF, e.g. \(F_{X}^{-1}(x)\)
3. Compute \(X=F_{X}^{-1}(u)\). The computed random variable \(X\) has distribution \(F_X(x)\)

Generate Random Point in a Circle

private double r, x, y;

public Solution(double radius, double x_center, double y_center) {
    this.r = radius;
    this.x = x_center;
    this.y = y_center;
}

public double[] randPoint() {
    // PDF: f(x) = 2 * r, R = 1
    // CDF: F(x) = r ^ 2
    // F' = sqrt(r)
    double d = r * Math.sqrt(Math.random());
    double theta = 2 * Math.random() * Math.PI;

    return new double[]{x + d * Math.cos(theta), y + d * Math.sin(theta)};
}

Reservoir Sampling

Reservoir sampling

Choosing a simple random sample, without replacement, of k items from a population of unknown size n in a single pass over the items.

Algorithm R:

/**
 * Reservoir sampling with Algorithm R.
 * @param nums input array
 * @param k reservoir size
 * @return output reservoir array with randomly chosen items
 */
public int[] reservoirSample(int[] nums, int k) {
    // fills the reservoir array
    for (int i = 0; i < k; i++) {
        r[i] = nums[i];
    }

    // replaces elements with gradually decreasing probability
    for (int i = k; i < nums.length; i++) {
        int j = rand.nextInt(i + 1);
        if (j < k) {
            r[j] = nums[i];
        }
    }
}

Random Pick Index

private int[] nums;
private Random rand;

public Solution(int[] nums) {
    this.nums = nums;
    this.rand = new Random();
}

public int pick(int target) {
    int index = -1, count = 0;
    // reservoir size == 1
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == target && rand.nextInt(++count) == 0) {
            index = i;
        }     
    }

    return index;
}

Linked List Random Node

Online Majority Element In Subarray

private Map<Integer, List<Integer>> map = new HashMap<>();
private int[] arr;
private Random rand = new Random();

public MajorityChecker(int[] arr) {
    this.arr = arr;
    for (int i = 0; i < arr.length; i++) {
        map.computeIfAbsent(arr[i], k -> new ArrayList<>()).add(i);
    }
}

// gets the number of occurrences of the given element in the range
private int getOccurrence(int left, int right, int a) {
    List<Integer> list = map.get(a);
    int i = Collections.binarySearch(list, left);
    if (i < 0) {
        i = ~i;
    }
    if (i == list.size()) {
        return 0;
    }

    int j = Collections.binarySearch(list, right);
    if (j < 0) {
        j = ~j - 1;
    }
    return j - i + 1;
}

private int getRandomNum(int l, int r) {
    return rand.nextInt(r - l + 1) + l;
}

public int query(int left, int right, int threshold) {
    // randomly picks an element in the range
    // attempts 10 times
    // probability of false negative < 0.5 ^ 20 ~= 1e-6
    for (int i = 0; i < 10; i++) {
        int a = arr[getRandomNum(left, right)];
        if (getOccurrence(left, right, a) >= threshold) {
            return a;
        }
    }
    return -1;
}