Monotonic Data Structure

Posted Nov 30, 2023 Updated Apr 11, 2024

By Qinghao Hou 34 min read

Overview

Form-I Template

The most commonly used template of monotonically strictly increasing stack is shown belown:

  
// Monotonically increasing stack (strict)
stack<int> st;
for (int i = 0; i < n; i++) {
    while (!st.empty() && nums[i] <= st.top()) {
        st.pop();
    }
    // It's also very common to push the index: st.push(i);
    st.push(nums[i]);
}

Variants:

Monotonically non-strictly increasing stack: nums[i] < st.top()
Monotonically strictly decreasing stack: nums[i] >= st.top()
Monotonically non-strictly decreasing stack: nums[i] > st.top()

Let’s go over the algorithm with an example [2,5,1,3,6,4]. The algorithm maintains a monotonically strictly increasing stack while iterating from left to right:

index	element	stack
0	2	`[2]`
1	5	`[2,5]`
2	1	`[1]`
3	3	`[1,3]`
4	6	`[1,3,6]`
5	4	`[1,3,4]`

Form-II Template

The other form of monotonic stack template looks more intuitive, but actually less commonly used:

  
// Monotonically increasing stack (strict)
stack<int> st;
for (int i = 0; i < n; i++) {
    if (st.empty() || nums[i] > st.top()) {
        st.push(nums[i]);
    }
}

With the same example [2,5,1,3,6,4], the stack of the algorithm changes as follows:

index	element	stack
0	2	`[2]`
1	5	`[2,5]`
2	1	`[2,5]`
3	3	`[2,5]`
4	6	`[2,5,6]`
5	4	`[2,5,6]`

In another perspective, the stack in this template stores the cumulative maximum of the sequence. Cumulative maximum funtion is monotonically increasing, so is the stack.

Maximum Width Ramp

  
public int maxWidthRamp(int[] nums) {
    int max = 0, n = nums.length;
    // Decreasing stack
    Deque<Integer> st = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        if (st.isEmpty() || nums[i] < nums[st.peek()]) {
            st.push(i);
        }
    }

    for (int i = n - 1; i > max; i--) {
        while (!st.isEmpty() && nums[i] >= nums[st.peek()]) {
            // i is the largest index such that nums[i] >= top
            // so, it's safe to pop
            max = Math.max(max, i - st.pop());
        }
    }
    return max;
}

Theorems and Corollaries

Let \(st(i)\) denote the stack of Form-I template when the iteration at index \(i\) is complete, we have the following theorem¹:

Define a sequence \(a_n = \min_{n \le j \le i}(\text{nums}[j])\), then \(st(i) = \text{dedupe}(a_n)\), where \(\text{dedupe}(a_n)\) is a function that de-duplicate the sequence \(a_n\) while preserving the order of sequence terms.

The below code implementation illustrates the theorem, and it uses a variant of the Form-II template:

  
vector<int> st;
for (int j = i; j >= 0; j--) {
    if (st.empty() || nums[j] < st.back()) {
        st.push_back(nums[j]);
    }
}

// Monotonically increasing stack (strict)
ranges::reverse(st);

Therefore, we can conclude that Form-I template and Form-II template are interconvertible.

It’s trivial to derive the following corollaries on Form-I template:

Corollary 1 The current element nums[i] is always at the top.

A direct conslusion of this corollary is: the condition nums[i] <= st.top() in the while loop always starts with nums[i] <= nums[i - 1], because nums[i - 1] is the stack top.

Corollary 2 The minimum element of nums[0...i] is always at the bottom.

Corollary 3 The stack is lexicographically minimum subsequence of nums[0...i].

Monotonic Stack

Lexicographic Order

Remove K Digits

  
string removeKdigits(string num, int k) {
    string t;
    for (const char& ch : num) {
        // Monotonically increasing stack
        while (k && !t.empty() && ch < t.back()) {
            t.pop_back();
            k--;
        }

        // To avoid leading 0, don't push '0' if the stack is empty
        if (!t.empty() || ch > '0') {
            t += ch;
        }
    }

    // Uses up k digits
    while (k && !t.empty()) {
        t.pop_back();
        k--;
    }
    return t.empty() ? "0" : t;
}

Find the Most Competitive Subsequence

  
public int[] mostCompetitive(int[] nums, int k) {
    int[] st = new int[k];
    // j is the stack size
    for (int i = 0, j = 0, n = nums.length; i < n; i++) {
        // (n - i) remaining numbers
        while (j > 0 && nums[i] < st[j - 1] && n - i + j > k) {
            j--;
        }
        if (j < k) {
            st[j++] = nums[i];
        }
    }
    return st;
}

PLE/PGE/NLE/NGE

Previous Less Element (PLE)
Previous Greater Element (PGE)
Next Less Element (NLE)
Next Greater Element (NGE)

The requested element can be strictly or non-strictly less/greater.

The template below uses monotonically increasing stack to get PLE/NLE.

  
Deque<Integer> st = new ArrayDeque<>();
int[] prev = new int[n], next = new int[n];
Arrays.fill(next, n);

for (int i = 0; i < n; i++) {
    // Monotonically increasing stack
    // Strictly less (<) next
    while (!st.isEmpty() && nums[i] < nums[st.peek()]) {
        next[st.pop()] = i;
    }
    // Non-strictly less (<=) prev
    prev[i] = st.isEmpty() ? -1 : st.peek();
    st.push(i);
}

	Previous <	Previous <=	Next <	Next <=
Monotonic Stack	Increasing	Increasing	Increasing	Increasing
Stack Strictness	Strict	Non-strict	Non-strict	Strict
Condition	a[i] <= top	a[i] < top	a[i] < top	a[i] <= top

From the theorem, we have the following conclusions for PLE and NLE²:

In the stack, each element is the PLE of the element on top of it.
After all iterations (\(i = n\)), \(st(n)\) is the set of elements that don’t have NLEs.
To get \(S_{\text{NLE}}(\text{nums}, i) = \{a \mid \text{NLE}(a) = \text{nums[i]} \}\), hold nums[i] and keep popping until \(\text{PLE}(\text{nums[i]})\):
1 2 3 while (!st.isEmpty() && nums[i] < nums[st.peek()]) { next[st.pop()] = i; }
To get \(S_{\text{PLE}}(\text{nums}, i) = \{a \mid \text{PLE}(a) = \text{nums[i]} \}\), iterate over nums from i until nums[i] is popped out of the stack, i.e., until \(\text{NLE}(\text{nums[i]})\):
1 prev[i] = st.isEmpty() ? -1 : st.peek();
- Before nums[i] is popped, at most one element of \(S_{\text{PLE}}(\text{nums}, i)\) is found at each index.
- Since PLE is NLE in reverse, we can iterate over nums backward and find NLE instead. Thus we find all elements of the set by computation at only one index i, rather than a range of indices.

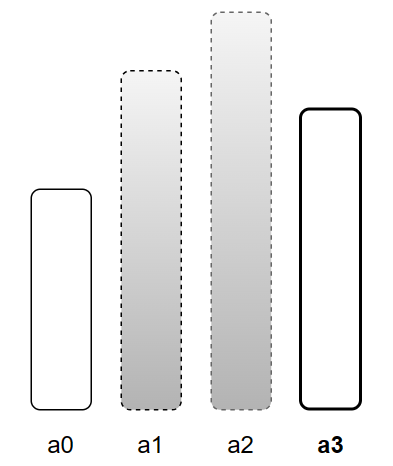Fig. 1. Monotonically increasing stack

In Fig. 1, a3 is the current element, and we have the following relations:

a0 = PLE(a1) = PLE(a3)
a1 = PLE(a2)
a3 = NLE(a1) = NLE(a2)
a0 and a3 don’t have NLEs

Similarly, with monotonically decreasing stack, we can get PGE/NGE.

	Previous >	Previous >=	Next >	Next >=
Monotonic Stack	Decreasing	Decreasing	Decreasing	Decreasing
Stack Strictness	Strict	Non-strict	Non-strict	Strict
Condition	a[i] >= top	a[i] > top	a[i] > top	a[i] >= top

Final Prices With a Special Discount in a Shop

  
vector<int> finalPrices(vector<int>& prices) {
    vector<int> answer = prices;
    // Next less element
    stack<int> st;
    for (int i = 0; i < prices.size(); i++) {
        while (!st.empty() && answer[i] <= answer[st.top()]) {
            answer[st.top()] -= answer[i];
            st.pop();
        }
        st.push(i);
    }
    return answer;
}

Next Greater Element IV

  
vector<int> secondGreaterElement(vector<int>& nums) {
    int n = nums.size();
    vector<int> answer(n, -1);

    // st1: elements that haven't found their first NGE
    // st2: elements that have found their first NGE but not second NGE
    stack<int> st1, st2, tmp;
    for (int i = 0; i < n; i++) {
        // Finds second NGE.
        // After the while loop, nums[i] <= st2.top().
        while (!st2.empty() && nums[i] > nums[st2.top()]) {
            answer[st2.top()] = nums[i];
            st2.pop();
        }

        // Moves all the elements whose first NGE is nums[i] to `tmp`.
        // `tmp` is a monotonically increasing stack, and nums[i] > tmp.top().
        while (!st1.empty() && nums[i] > nums[st1.top()]) {
            tmp.push(st1.top());
            st1.pop();
        }

        // nums[i] <= st2.top()
        // nums[i] > tmp.top()
        // => st2.top > tmp.top()
        // So, we can push tmp reversely to st2, and st2 remains monotonically decreasing.
        while (!tmp.empty()) {
            st2.push(tmp.top());
            tmp.pop();
        }

        st1.push(i);
    }
    return answer;
}

Generalization: K-th Greater Element

  
vector<int> secondGreaterElement(vector<int>& nums, int k = 2) {
    int n = nums.size();
    vector<int> answer(n, -1);
    vector<stack<int>> sts(k);
    stack<int> tmp;
    for (int i = 0; i < n; i++) {
        for (int j = k - 1; j > 0; j--) {
            while (!sts[j].empty() && nums[i] > nums[sts[j].top()]) {
                answer[sts[j].top()] = nums[i];
                sts[j].pop();
            }

            while (!sts[j - 1].empty() && nums[i] > nums[sts[j - 1].top()]) {
                tmp.push(sts[j - 1].top());
                sts[j - 1].pop();
            }

            while (!tmp.empty()) {
                sts[j].push(tmp.top());
                tmp.pop();
            }
        }
        sts[0].push(i);
    }
    return answer;
}

O(nlog(n)) solution: monotonic stack + piority queue/binary search

Minimum Difficulty of a Job Schedule

  
// O(nd)
int minDifficulty(vector<int>& jobDifficulty, int d) {
    int n = jobDifficulty.size();
    if (n < d) {
        return -1;
    }

    // Rolling DP
    // Initializes dp with max jobDifficulty of each day
    vector<int> dp(n, 1000);

    // With stack, we don't have to try all cuts
    stack<int> st;
    for (int i = 0, prev = 0; i < d; prev = dp[i++]) {
        // Clears the stack
        st = {};

        // dp[j]: min difficulty of a schedule after first i days with (j + 1) jobs.
        // dp is non-decreasing.
        // For dp[j], the j-th job is always in the last bucket.
        for (int j = i; j < n; j++) {
            swap(prev, dp[j]);

            // dp has i buckets.
            // Initializes the dp for the new i by adding a new bucket and putting the j-th job into it
            // (we can possibly find better solutions with stack later).
            // Now there are (i + 1) buckets.
            dp[j] += jobDifficulty[j];

            // Monotonically decreasing stack
            // Finds the job in the last bucket that is less difficulty than the j-th job.
            // (jobDifficulty[j] - jobDifficulty[top]) is the extra difficulty introduced by the j-th job.
            // Apparently, for the ones in the last bucket that are more difficulty than the j-th job,
            // the j-th job won't affect their dp value. So we skip them.
            // We only process elements whose NGE is jobDifficulty[j], not all the previous jobs that are of less difficulty,
            // because those jobs had been processed by an earlier index m (i <= m < j), and m remains in the stack (m doesn't have NGE)
            while (!st.empty() && jobDifficulty[j] >= jobDifficulty[st.top()]) {
                int top = st.top();
                dp[j] = min(dp[j], dp[top] + jobDifficulty[j] - jobDifficulty[top]);
                st.pop();
            }

            // For all the indices k before p = PGE(j), dp[k] <= dp[p]
            if (!st.empty()) {
                dp[j] = min(dp[j], dp[st.top()]);
            }

            st.push(j);
        }
    }
    return dp[n - 1];
}

Number of Visible People in a Queue

  
public int[] canSeePersonsCount(int[] heights) {
    int n = heights.length;
    int[] answer = new int[n];
    Deque<Integer> st = new ArrayDeque<>();
    // There are two types of people that the i-th person can see to his right:
    // 1. NGE(i) (>=). All the people to the right of NGE(i) are blocked by it and thus invisible.
    // 2. The people in the range of (i, NGE(i)), and their PGE is i.
    //    If j in (i, NGE(i)) and PGE(j) > i, then i is blocked by PGE(j) and thus invisible to j.
    for (int i = 0; i < n; i++) {
        // Monotonically decreasing stack (strict)
        // Next greater (>=) element
        while (!st.isEmpty() && heights[i] >= heights[st.peek()]) {
            // st.peek() can see i
            // st.peek() can't see after i, so st.peek() is done and popped
            answer[st.pop()]++;
        }

        if (!st.isEmpty()) {
            // Previous greater (>) element
            // st.peek() can see i
            answer[st.peek()]++;
        }

        st.push(i);
    }
    return answer;
}

In this problem, elements are not necessarily distinct. Therefore, we need to make a slight change to the code:

  
public int[] canSeePersonsCount(int[] heights) {
    int n = heights.length;
    int[] answer = new int[n];
    Deque<Integer> st = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        // monotonically decreasing stack (strict)
        // next greater (>=) element
        boolean isEqual = false;
        while (!st.isEmpty() && heights[i] >= heights[st.peek()]) {
            if (heights[i] == heights[st.peek()]) {
                isEqual = true;
            }
            // st.peek() can see i
            // st.peek() can't see after i, so st.peek() is done and popped
            answer[st.pop()]++;
        }

        // e.g. [4,2,1,1,3]
        // we skip incrementing the answer at index 0 when i == 3
        // because it's already incremented when i == 2
        // iwo, heights[0] can't see heights[3] because of heights[2]
        if (!st.isEmpty() && isEqual) {
            // previous greater (>) element
            // st.peek() can see i
            answer[st.peek()]++;
        }

        st.push(i);
    }
    return answer;
}

Increasing/Decreasing Spanning Forest

Imagine each element is a node in a graph, and we connect node u to its NLE node v with an edge. The resulting graph is an increasing spanning forest.

Fig. 2. Increasing/Decreasing spanning forest

Online Stock Span

  
private Deque<int[]> st;

public StockSpanner() {
    this.st = new ArrayDeque<>();
}

public int next(int price) {
    int count = 1;
    // Next greater element
    while (!st.isEmpty() && price >= st.peek()[0]) {
        count += st.pop()[1];
    }
    st.push(new int[]{price, count});
    return count;
}

Can you see the connection between the above solution and Tree recursion (DFS)?

Minimum Cost Tree From Leaf Values

  
int mctFromLeafValues(vector<int>& arr) {
    stack<int> st;
    st.push(numeric_limits<int>::max());

    int sum = 0;
    for (int a : arr) {
        // If a leaf has both PGE and NGE, removes it and multiplies it with the smaller of the two.
        while (st.top() <= a) {
            int top = st.top();
            st.pop();
            sum += top * min(st.top(), a);
        }
        st.push(a);
    }

    // The remaining leaves don't have an NGE.
    // Starts from the top since the stack is decreasing.
    while (st.size() > 2) {
        int top = st.top();
        st.pop();
        sum += st.top() * top;
    }
    return sum;
}

In fact, Fig.2 shows how to span the tree from the leaves if we always pick NLE.

Iteration Direction

132 Pattern

  
bool find132pattern(vector<int>& nums) {
    stack<int> st;
    // e1 e3 e2 -> 1 3 2
    int e2 = numeric_limits<int>::min();
    for (int i = nums.size() - 1; i >= 0; i--) {
        // nums[i] as e1
        if (nums[i] < e2) {
            return true;
        }

        // The following algorithm ensures when nums[i] > e2,
        // if j is the largest index such that j < i and nums[j] < e2,
        // we will find a 132 pattern with nums[j] as e1.
        // Proof:
        // Case 1: nums[i] > e3 (= st.top())
        //   The pattern now is 321.
        //   After stack operations, e2 <- e3, e3 <- nums[i].
        //   Both e2 and e3 increase, nums[j] < e2 < e3 (132 pattern).
        // Case 2: e2 < nums[i] < e3
        //   The pattern now is 231.
        //   After stack operations, e3 <- nums[i]
        //   e2 remains unchanged, e3 decreases, nums[j] < e2 < e3 (132 pattern).
        // Case 3: nums[i] == e3
        //   The pattern now is 221.
        //   After stack operations, e3 <- nums[i].
        //   Both e2 and e3 remain unchanged, nums[j] < e2 < e3 (132 pattern).
        // Case 4: nums[i] == e2
        //   The pattern now is 121.
        //   After stack operations, e3 <- nums[i].
        //   e2 remains unchanged, e3 decreases, nums[j] < e2 == e3 (122 pattern).
        //   Then for the next element, the 122 pattern possibly transitions to:
        //   a) Case 1, back to 132 pattern
        //   b) Case 4, remains 122 pattern
        //   It it stays in 122 pattern until index j, we can say 132 pattern exists (with nums[j] as e1),
        //   because there existed an e3' > e3 == e2
        // In summary, e2 and e3 are non-decreasing, and e3 >= e2 always stands

        // Monotonically decreasing stack (reverse)
        // Finds the largest e2 when nums[i] is viewed as e3
        while (!st.empty() && nums[i] > st.top()) {
            e2 = st.top();
            st.pop();
        }
        st.push(nums[i]);
    }
    return false;
}

Steps to Make Array Non-decreasing

  
int totalSteps(vector<int>& nums) {
    // All elements will be removed by their PGEs.
    // {num, number of steps performed until `num` is removed by its PGE (>)}
    stack<pair<int,int>> st;
    int mx = 0;
    for (int num : nums) {
        int steps = 0;
        while (!st.empty() && num >= st.top().first) {
            // Gets max steps among all the popped elements.
            steps = max(steps, st.top().second);
            st.pop();
        }

        // If previous greater (>) element exists, removing `num` increments steps by one
        st.push({num, steps = st.empty() ? 0 : steps + 1});
        mx = max(mx, steps);
    }
    return mx;
}

Forward PGE = Backward NGE

Equivalently, we can build a monotonically decreasing stack by backward iteration:

  
int totalSteps(vector<int>& nums) {
    // {num, number of steps performed `num` needs to remove all the elements whose NGE (>) is `num`}
    stack<pair<int,int>> st;
    int mx = 0;
    for (int i = nums.size() - 1; i >= 0; i--) {
        int steps = 0;
        while (!st.empty() && nums[i] > st.top().first) {
            // Say, it takes `num` t0 steps to meet a to-be-popped element (denoted by e),
            // and st[e][1] = t1.
            // The number of steps for `num` to remove e is max(t0, t1).
            // t0 > t1
            // e.g. [10,6,7,2,8], num = 10, e = 7, t0 = 2, t1 = 1
            //   * Step 1: 10 <- 6, 7 <- 2
            //   * Step 2: 10 <- 7
            //   * Step 3: 10 <- 8
            // t0 < t1
            // e.g. [10,6,2,3,8], num = 10, e = 6, t0 = 1, t1 = 2
            //   * Step 1: 10 <- 6, 6 <- 2
            //   * Step 2: 10 <- 3 (imagine 10 helps 6 to finish its remaining task)
            //   * Step 3: 10 <- 8
            //
            // `steps`: the number of steps `num` needs to meet this to-be-popped element.
            // steps + 1 is required for `num` to move from this to the next to-be-popped element.
            steps = max(steps + 1, st.top().second);
            st.pop();
        }
        st.push({nums[i], steps});
        mx = max(mx, steps);
    }
    return mx;
}

The following problem is not PGE or NGE, and the solution doesn’t use stacks. But we can see some similarities.

Sum of Imbalance Numbers of All Subarrays

  
int sumImbalanceNumbers(vector<int>& nums) {
    // In an array, if `num` has next greater element that's not `num + 1`,
    // then `num` contributes one score to the imbalance of the array.
    int sum = 0, n = nums.size();
    // lastIndices[num]: index of the last occurrence `num`
    // leftBounds[num]: all the subarrays of (leftBounds[num], num] don't contain (num + 1).
    //    Therefore, for any one of the subarrays, if `num` is not the max value,
    //    then `num` contributes one score to the imbalance of the subarray.
    vector<int> lastIndices(n + 2, -1), leftBounds(n);

    for (int i = 0; i < n; i++) {
        // `lastIndices[nums[i]]` is used for deduplication.
        // If a subarray contains multiple nums[i], only one of them constributes to the imbalance of the subarray.
        leftBounds[i] = max(lastIndices[nums[i] + 1], lastIndices[nums[i]]);
        lastIndices[nums[i]] = i;
    }

    ranges::fill(lastIndices, n);
    for (int i = n - 1; i >= 0; i--) {
        lastIndices[nums[i]] = i;
        sum += (i - leftBounds[i]) * (lastIndices[nums[i] + 1] - i);
    }

    // Subtracts the result when nums[i] is the max of the subarray.
    // Each subarray has a max, and each subarray contributes to the imbalance sum as per the algorithm above.
    // There are n * (n + 1) / 2 subarrays in total.
    return sum - n * (n + 1) / 2;
}

Subarray Min/Max

Sum of Subarray Minimums

The basic idea is to find both the previous and next less elements of each array element with two stacks. This can be simplified to one stack:

  
int sumSubarrayMins(vector<int>& arr) {
    int res = 0, n = arr.size();
    const int mod = 1e9 + 7;
    stack<int> st;
    // Virtually appends 0 to the end of the array
    for (int i = 0; i <= n; i++) {
        while (!st.empty() && (i == n || arr[i] < arr[st.top()])) {
            // i is the next less (<) element of j
            int j = st.top();
            st.pop();
            // k is the previous less (<=) element of j
            int k = st.empty() ? -1 : st.top();
            res = (res + (long long)arr[j] * (i - j) * (j - k)) % mod;
        }
        st.push(i);
    }
    return res;
}

Subarray With Elements Greater Than Varying Threshold

  
if ((i - k - 1) * nums[j] > threshold) {
    return i - k - 1;
}

With this perspective, the solution of the following Histogram problem is much easier to understand:

Largest Rectangle in Histogram

  
int largestRectangleArea(vector<int>& heights) {
    // Indices of non-descreasing heights
    stack<int> st;
    st.push(-1);  // makes width concise

    int area = 0, n = heights.size();
    for (int i = 0; i <= n; i++) {
        while (st.top() >= 0 && (i == n || heights[i] < heights[st.top()])) {
            // j = st.pop()
            // heights[i] is the next less (<) element of heights[j]
            int h = heights[st.top()];
            st.pop();
            // k = st.top()
            // heights[k] is the previous less (<=) element of heights[j]
            // w = length of (k, i)
            int w = i - 1 - st.top();
            area = max(area, h * w);
        }
        st.push(i);
    }
    return area;
}

[2,1,5,6,2,3]
i = 0	[0]				area = 0
i = 1	[]		h * w = 2	area = 2
i = 1	[1]				area = 2
i = 2	[2,1]				area = 2
i = 3	[3,2,1]				area = 2
i = 4	[2,1]		h * w = 6	area = 6
i = 4	[1]		h * w = 10	area = 10
i = 4	[4,1]				area = 10
i = 5	[5,4,1]				area = 10
i = 6	[4,1]		h * w = 3	area = 10
i = 6	[1]		h * w = 8	area = 10
i = 6	[]		h * w = 6	area = 10
i = 6	[6]				area = 10

Maximum of Minimum Values in All Subarrays

  
public int[] findMaximums(int[] nums) {
    int n = nums.length;
    int[] ans = new int[n];

    Deque<Integer> st = new ArrayDeque<>();
    // virtually appends 0 to the end of the array
    for (int i = 0; i <= n; i++) {
        while (!st.isEmpty() && (i == n || nums[i] < nums[st.peek()])) {
            // nums[i] is the next less (<) element of nums[j]
            int j = st.pop();
            // k = st.peek()
            // nums[k] is the previous less (<=) element of nums[j]
            // the range is (k, i)
            int len = i - (st.isEmpty() ? -1 : st.peek()) - 1;
            ans[len - 1] = Math.max(ans[len - 1], nums[j]);
        }
        st.push(i);
    }

    // ans is non-increasing
    for (int i = n - 1; i > 0; i--) {
        ans[i - 1] = Math.max(ans[i - 1], ans[i]);
    }
    return ans;
}

Monoqueue

Sliding Window Min/Max

Similar to that in sliding window, the constraint function \(h(m)\) is monotonically decreasing. Monoqueues can be used to find the min/max of a window constrained by a monotonically decreasing function.

Sliding Window Maximum

  
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    int n = nums.size();
    vector<int> res;
    deque<int> dq;
    for (int i = 0; i < n; i++) {
        // Removes the out-of-window number
        if (!dq.empty() && dq.front() == i - k) {
            dq.pop_front();
        }

        // Monotonically decreasing from head to tail
        while (!dq.empty() && nums[i] > nums[dq.back()]) {
            dq.pop_back();
        }
        dq.push_back(i);

        if (i >= k - 1) {
            res.push_back(nums[dq.front()]);
        }
    }
    return res;
}

The above solution is a good example of the application of Property #2:

Equivalently, we can always use priority queues to solve this type of problem. In the following example, we store [value, position] pairs in the heap, and pops elements until the distance is within the required range:

Max Value of Equation

Monoqueue:

  
public int findMaxValueOfEquation(int[][] points, int k) {
    // yi + yj + |xi - xj|
    // = yi + yj + xj - xi
    // = (yi - xi) + (xj + yj)

    // {yi - xi , xi}
    Deque<int[]> dq = new ArrayDeque<>();

    int max = Integer.MIN_VALUE;
    for (int[] p : points) {
        while (!dq.isEmpty() && p[0] - dq.peekFirst()[1] > k) {
            dq.pollFirst();
        }
        if (!dq.isEmpty()) {
            max = Math.max(max, dq.peekFirst()[0] + p[0] + p[1]);
        }

        // monotonically decreasing (from first to last)
        while (!dq.isEmpty() && p[1] - p[0] > dq.peekLast()[0]) {
            dq.pollLast();
        }
        dq.offerLast(new int[]{p[1] - p[0], p[0]});
    }
    return max;
}

Priority Queue:

  
public int findMaxValueOfEquation(int[][] points, int k) {
    // yi + yj + |xi - xj|
    // = yi + yj + xj - xi
    // = (yi - xi) + (xj + yj)

    // {yi - xi , xi}
    Queue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> -a[0]));

    int max = Integer.MIN_VALUE;
    for (int[] p : points) {
        while (!pq.isEmpty() && p[0] - pq.peek()[1] > k) {
            pq.poll();
        }
        if (!pq.isEmpty()) {
            max = Math.max(max, pq.peek()[0] + p[0] + p[1]);
        }
        pq.offer(new int[]{p[1] - p[0], p[0]});
    }
    return max;
}

Maximum Number of Robots Within Budget

See Sliding window (monotonically decreasing function) for the sliding window template.

  
public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
    long sum = 0;
    int i = 0, j = 0, n = chargeTimes.length;
    Deque<Integer> dq = new LinkedList<>();
    while (j < n) {
        sum += runningCosts[j];

        // Monotonically decreasing
        while (!dq.isEmpty() && chargeTimes[j] >= chargeTimes[dq.peekLast()]) {
            dq.pollLast();
        }
        dq.offerLast(j++);

        // Moves i forward
        if (chargeTimes[dq.peekFirst()] + (j - i) * sum > budget) {
            if (dq.peekFirst() == i) {
                dq.pollFirst();
            }
            sum -= runningCosts[i++];
        }
    }

    // Sliding window doesn't shrink
    return j - i;
}

Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

  
int longestSubarray(vector<int>& nums, int limit) {
    deque<int> maxd, mind;
    int i = 0, j = 0;
    while (j < nums.size()) {
        while (!maxd.empty() && maxd.back() < nums[j]) {
            maxd.pop_back();
        }
        maxd.push_back(nums[j]);

        while (!mind.empty() && mind.back() > nums[j]) {
            mind.pop_back();
        }
        mind.push_back(nums[j]);
        j++;

        if (maxd.front() - mind.front() > limit) {
            if (maxd.front() == nums[i]) {
                maxd.pop_front();
            }
            if (mind.front() == nums[i]) {
                mind.pop_front();
            }
            i++;
        }
    }
    return j - i;
}

This technique can be used to compute the recurrence relation more quickly in some dynamic programming problems.

Jump Game VI

  
public int maxResult(int[] nums, int k) {
    int n = nums.length;
    // dp[i]: max score to reach the end starting at index i
    int[] dp = new int[n];
    dp[n - 1] = nums[n - 1];

    Deque<Integer> dq = new ArrayDeque<>();
    for (int i = n - 2; i >= 0; i--) {
        // max(dp[i + 1, i + k])
        if (!dq.isEmpty() && dq.peek() == i + k + 1) {
            dq.poll();
        }

        while (!dq.isEmpty() && dp[i + 1] > dp[dq.peekLast()] {
            dq.pollLast();
        }
        dq.offer(i + 1);

        // Finds max using monoqueue
        dp[i] = nums[i] + dp[dq.peek()];
    }
    return dp[0];
}

In the solution above, it’s worth noting the iteration is in reverse order, which is more intuitive and straightforward than the natural order.

Similar problem: Constrained Subsequence Sum.

Shortest Subarray With Sum >= k

In this type of problems, there is a constraint \(f(i,j) \ge 0\), where \(i\) is the current index and \(j\) is a smaller index. For all indices \(\in (j, i)\), \(f(i,j) \lt 0\). Monoqueues can be used to find the largest \(j\) of each \(i\) which satisfies the constraint.

Shortest Subarray with Sum at Least K

  
public int shortestSubarray(int[] nums, int k) {
    int n = nums.length;
    // Prefix sum
    int[] p = new int[n + 1];
    for (int i = 0; i < n; i++) {
        p[i + 1] = p[i] + nums[i];
    }

    // Finds the smallest j - i so that j > i and p[j] - p[i] >= k
    // We call p[j] minuend and p[i] subtrahend
    int min = n + 1;
    // Strictly increasing monoqueue
    Deque<Integer> dq = new ArrayDeque<>();
    for (int i = 0; i < p.length; i++) {
        // Checks all possible candidates when p[i] is used as the minuend.
        // Pops the head of the deque until p[i] - p[head] < k.
        // The head is a possible candidate.
        while (!dq.isEmpty() && p[i] - p[dq.peekFirst()] >= k) {
            min = Math.min(min, i - dq.pollFirst());
        }

        // The current head is the min in the range of [current head, i],
        // so for all j in this range, p[i] - p[j] < k.
        // Therefore, there's no shorter subarray.
        while (!dq.isEmpty() && p[i] <= p[dq.peekLast()]) {
            dq.pollLast();
        }
        dq.offerLast(i);
    }

    return min <= n ? min : -1;
}

Find Maximum Non-decreasing Array Length

  
int findMaximumLength(vector<int>& nums) {
    // dp[i]: max len of a non-decreasing array after applying operations for the first i elements in nums
    // dp[i] = max(dp[j]) + 1, where 0 < j < i and sum(nums[j...(i - 1)]) >= last[j]
    //   last[j] is the last element after applying operations to the first j elements in nums
    //
    // dp[i] is non-decreasing, because we can always append nums[i] to the non-decreasing array
    // converted from nums[0...(i - 1)] and it's still valid. Therefore:
    //
    // dp[i] = dp[j] + 1, where j is the highest index that satisfies:
    //   - 0 < j < i
    //   - p[i] - p[j] >= last[j] (prefix sum) => last[j] + p[j] <= p[i]
    int n = nums.size();
    vector<long long> p(n + 1);
    for (int i = 0; i < n; i++) {
        p[i + 1] = p[i] + nums[i];
    }

    vector<int> dp(n + 1), last(n + 1);
    deque<int> dq;
    for (int i = 1, j = 0; i <= n; i++) {
        // For every index k in the deque, last[k] + p[k] > p[i]
        while (!dq.empty() && last[dq.front()] + p[dq.front()] <= p[i]) {
            j = dq.front();
            dq.pop_front();
        }

        dp[i] = dp[j] + 1;
        last[i] = p[i] - p[j];

        // Monotonically increasing queue
        while (!dq.empty() && last[i] + p[i] <= last[dq.back()] + p[dq.back()]) {
            dq.pop_back();
        }
        dq.push_back(i);
    }
    return dp[n];
}

Monotonic Map

Maximum Balanced Subsequence Sum

  
long long maxBalancedSubsequenceSum(vector<int>& nums) {
    map<int, long long> mp{{numeric_limits<int>::min(), 0}};
    for (int i = 0; i < nums.size(); i++) {
        // Considers positive num only
        if (nums[i] > 0) {
            auto it = mp.upper_bound(nums[i] - i);
            long long sum = nums[i] + prev(it)->second;
            mp.insert_or_assign(it, nums[i] - i, sum);
            // Monotonically increasing values
            // Because greater keys with less values are no better than current
            while (it != end(mp) && it->second <= sum) {
                mp.erase(it++);
            }
        }
    }
    return mp.size() > 1 ? rbegin(mp)->second : *max_element(begin(nums), end(nums));
}

Maximum Sum Queries

  
// {y: x + y}, ascending
// candidates for the current query
// monotonic map: keys are ascending, while values are descending
private TreeMap<Integer, Integer> map = new TreeMap<>();

public int[] maximumSumQueries(int[] nums1, int[] nums2, int[][] queries) {
    int n = nums1.length, m = queries.length;
    Integer[] numIndices = new Integer[n], queryIndices = new Integer[m];
    for (int i = 0; i < n; i++) {
        numIndices[i] = i;
    }
    for (int i = 0; i < m; i++) {
        queryIndices[i] = i;
    }

    // iterates nums in descending order of x
    // so we add candidate pairs to map as x decreases, rather than remove candiate pairs
    Arrays.sort(numIndices, Comparator.comparingInt(i -> -nums1[i]));
    Arrays.sort(queryIndices, Comparator.comparingInt(i -> -queries[i][0]));

    int[] answer = new int[m];
    for (int i = 0, j = 0; i < m; i++) {
        int queryIndex = queryIndices[i];
        // "nums1[j]" >= xi
        while (j < n && nums1[numIndices[j]] >= queries[queryIndex][0]) {
            int numIndex = numIndices[j];
            update(nums2[numIndex], nums1[numIndex] + nums2[numIndex]);
            j++;
        }
        // query(yi)
        answer[queryIndices[i]] = query(queries[queryIndex][1]);
    }
    return answer;
}

private void update(int y, int xy) {
    // if the candicates map already contains key y' >= y
    // then x' + y' >= current x + y, as x is in descending order
    // there is no need to put the current pair (y, x + y)
    var e = map.ceilingEntry(y);
    if (e != null && e.getValue() >= xy) {
        return;
    }

    // maintains map values as monotically decreasing
    // just like monotic stack
    e = map.floorEntry(y);
    while (e != null && e.getValue() <= xy) {
        map.remove(e.getKey());
        e = map.floorEntry(y);
    }
    map.put(y, xy);
}

// filters entries with key >= y only
private int query(int y) {
    var e = map.ceilingEntry(y);
    return e == null ? -1 : e.getValue();
}

+ Binary Search

Find Building Where Alice and Bob Can Meet

  
vector<int> leftmostBuildingQueries(vector<int>& heights, vector<vector<int>>& queries) {
    int m = queries.size();
    // Sorts queries in descending order of `b`,
    // so we process the heights from right to left.
    vector<int> indices, res(m);
    for (int i = 0; i < m; i++) {
        // a <= b
        int a = *ranges::min_element(queries[i]), b = *ranges::max_element(queries[i]);

        if (a == b || heights[a] < heights[b]) {
            res[i] = b;
        } else {
            indices.push_back(i);
        }
    }
    ranges::sort(indices, greater<int>(), [&](int i){ return *ranges::max_element(queries[i]); });

    vector<int> st;
    int j = heights.size() - 1;
    for (const int& i : indices) {
        int a = *ranges::min_element(queries[i]), b = *ranges::max_element(queries[i]);

        // Pushes [j:(b - 1):-1] to maintain a monotonic stack
        while (j >= b) {
            while (!st.empty() && heights[j] >= heights[st.back()]) {
                st.pop_back();
            }
            st.push_back(j--);
        }

        // Binary search
        auto it = upper_bound(rbegin(st), rend(st), a, [&](int i, int j){ return heights[i] < heights[j]; });
        res[i] = it == rend(st) ? -1 : *it;
    }

    return res;
}

For the sake of simplicity, we assume a) the stack is monotonically strictly increasing stack, b) all the elements are unique. It’s trivial to extend it to non-strict or descreasing stacks. ↩
Again, we don’t elaborate on PGE & NGE, or stack strictness. ↩

algorithm

This post is licensed under CC BY 4.0 by the author.