Mathematics
Theorem
Lagrange’s four-square theorem
Lagrange’s four-square theorem, also known as Bachet’s conjecture, states that every natural number can be represented as the sum of four integer squares. That is, the squares form an additive basis of order four.
\[p=a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{3}^{2}\]Legendre’s three-square theorem
Legendre’s three-square theorem states that a natural number can be represented as the sum of three squares of integers
\[n=x^{2}+y^{2}+z^{2}\]if and only if \(n\) is not of the form \(n = 4^a(8b + 7)\) for nonnegative integers \(a\) and \(b\).
An integer greater than one can be written as a sum of two squares if and only if its prime decomposition contains no prime congruent to 3 modulo 4 raised to an odd power.
Zeller’s congruence is an algorithm devised by Christian Zeller to calculate the day of the week for any Julian or Gregorian calendar date.
Gregorian calendar: \(h=\left(q+\left\lfloor {\frac {13(m+1)}{5}}\right\rfloor +K+\left\lfloor {\frac {K}{4}}\right\rfloor +\left\lfloor {\frac {J}{4}}\right\rfloor -2J\right){\bmod {7}}\)
\[\left\lceil {\frac {n}{m}}\right\rceil =\left\lfloor {\frac {n+m-1}{m}}\right\rfloor =\left\lfloor {\frac {n-1}{m}}\right\rfloor +1\] \[\left\lfloor {\frac {n}{m}}\right\rfloor =\left\lceil {\frac {n-m+1}{m}}\right\rceil =\left\lceil {\frac {n+1}{m}}\right\rceil -1\]\[|A\cup B|=|A|+|B|-|A\cap B|\]1
2
3
4
5
6
7
8
9
10
11
12
13
public int maxA(int N) {
// https://oeis.org/A178715
int[] dp = new int[N + 1];
for (int i = 0; i <= N; i++) {
dp[i] = i;
// j steps to reach maxA(j)
// then uses the remaining n - j steps to reach n - j - 1 copies of maxA(j)
for (int j = 1; j <= i - 3; j++) {
dp[i] = Math.max(dp[i], dp[j] * (i - j - 1));
}
}
return dp[N];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int[][] multiply(int[][] A, int[][] B) {
int m = A.length, n = B[0].length;
int[][] result = new int[m][n];
for (int i = 0; i < m; i++) {
for (int k = 0; k < B.length; k++) {
if (A[i][k] != 0) {
for (int j = 0; j < n; j++) {
if (B[k][j] != 0) {
result[i][j] += A[i][k] * B[k][j];
}
}
}
}
}
return result;
}
Non-negative Integers without Consecutive Ones
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public int findIntegers(int n) {
// Fibonacci
// f[i]: the number of integers whose binary representation is not more than i bits
// and do not contain cosecutive ones
int[] f = new int[32];
f[0] = 1;
f[1] = 2;
// e.g. i == 5
// [00000 - 11111] = [00000 - 01111] and [10000 - 10111]
// (any integer >= 11000 is not allowed)
// [00000 - 01111] => [0000 - 1111] = f[4]
// [10000 - 10111] => [000 - 111] = f[3]
// therefore, f[5] == f[4] + f[3]
for (int i = 2; i < f.length; i++) {
f[i] = f[i - 1] + f[i - 2];
}
// 2 ^ 30 > 10 ^ 9
// scans from MSB to LSB
int i = 30, sum = 0, prev = 0;
while (i >= 0) {
if ((n & (1 << i)) != 0) {
// sets current bit to zero
// so the following range is [000...0, 011...1] = f[i]
sum += f[i];
// two consecutive ones appears
if (prev == 1) {
// removes n itself
sum--;
break;
}
prev = 1;
} else {
prev = 0;
}
i--;
}
// adds extra 1 if there are no consecutive ones in n
return sum + 1;
}
1
2
3
4
5
6
7
1011010
1st bit: 0000000 - 0111111 -> f[6]
3rd bit: 1000000 - 1001111 -> f[4]
4th bit: 1010000 - 1010111 -> f[3]
anything greater than 1010111 will not be allowed
Catalan Number
The nth Catalan number is given directly in terms of binomial coefficients by
\[C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}=\prod \limits _{k=2}^{n}{\frac {n+k}{k}}\qquad {\text{for }}n\geq 0\] \[C_{0}=1\quad {\text{and}}\quad C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n}\]1
dp[n + 1] = dp[0] * dp[n] + dp[1] * dp[n - 1] + ... + dp[n] * dp[0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private static final int MOD = (int)1e9 + 7;
public int numberOfWays(int num_people) {
int n = num_people / 2; // pairs
long[] dp = new long[n + 1];
dp[0] = 1;
// splits pairs
for (int k = 1; k <= n; k++) {
for (int i = 0; i < k; i++) {
dp[k] = (dp[k] + dp[i] * dp[k - 1 - i]) % MOD;
}
}
return (int)dp[n];
}
Exponentiation
Exponentiation by squaring: square-and-multiply/binary exponentiation/double-and-add
\[x^{n}= \begin{cases} x\,(x^{2})^{\frac {n-1}{2}},&{\mbox{if }}n{\mbox{ is odd}} \\ (x^{2})^{\frac {n}{2}},&{\mbox{if }}n{\mbox{ is even}} \end{cases}\]If we write \(n\) in binary as \(b_{k}\cdots b_{0}\), then this is equivalent to defining a sequence \(r_{k+1}, \ldots, r_{0}\) by letting \(r_{k+1} = 1\) and then defining \(r_{i}=r_{i+1}^{2}x^{b_{i}}\) for \(i = k, \ldots, 0\), where \(r_{0}\) will equal \(x^{n}\).
| \(n=13\) | \(1\) | \(1\) | \(0\) | \(1\) | |
|---|---|---|---|---|---|
| \(x\) | \(x^8\) | \(x^4\) | \(x^2\) | \(x^1\) | |
| \(r\) | \(x^{13}\) | \(x^5\) | \(x^1\) | \(x^1\) | \(x^0\) |
Iterative:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public double myPow(double x, int n) {
// if n == Integer.MIN_VALUE, -n would overflow
// so n is converted to long
long nl = n;
if (nl < 0) {
x = 1 / x;
nl = -nl;
}
// fast power algorithm
// r = x ^ 0
double r = 1, pow = x;
for (long i = nl; i > 0; i /= 2) {
if (i % 2 == 1) {
r *= pow;
}
pow *= pow;
}
return r;
}
Recursive:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public double myPow(double x, int n) {
return fastPow(x, (long)n);
}
// fast power algorithm
private double fastPow(double x, long n) {
if (n < 0) {
return fastPow(1 / x, -n);
}
if (n == 0) {
return 1;
}
if (n == 1) {
return x;
}
return n % 2 == 0 ? fastPow(x * x, n / 2) : x * fastPow(x * x, (n - 1) / 2);
}
Another way of the last return is:
1
2
double half = fastPow(x, n / 2);
return half * half * (n % 2 == 0 ? 1 : x);
Radix
1
2
3
public int newInteger(int n) {
return Integer.parseInt(Integer.toString(n, 9));
}
Check if Number is a Sum of Powers of Three
1
2
3
4
5
6
7
8
9
10
11
public boolean checkPowersOfThree(int n) {
while (n > 0) {
if (n % 3 == 2) {
return false;
}
// right shifts ternary bits by 1
n /= 3;
}
return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int[] addNegabinary(int[] arr1, int[] arr2) {
int carry = 0, i = arr1.length - 1, j = arr2.length - 1;
Deque<Integer> st = new ArrayDeque<>();
while (i >= 0 || j >= 0 || carry != 0) {
if (i >= 0) {
carry += arr1[i--];
}
if (j >= 0) {
carry += arr2[j--];
}
st.push(carry & 1);
// carry = carry / (-2)
// carry can be -1, and -(carry >> 1) will be 1
carry = -(carry >> 1);
}
// clears leading zeros
while (st.size() > 1 && st.peek() == 0) {
st.pop();
}
return st.stream().mapToInt(a -> a).toArray();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int divide(int dividend, int divisor) {
if (dividend == Integer.MIN_VALUE && divisor == -1) {
return Integer.MAX_VALUE;
}
// long division in base-2
int a = Math.abs(dividend), b = Math.abs(divisor), result = 0;
for (int i = 31; i >= 0; i--) {
if ((a >>> i) - b >= 0) {
result += 1 << i;
a -= b << i;
}
}
return (dividend ^ divisor) >= 0 ? result : -result;
}
From \eqref{eq:1} and \eqref{eq:2},
\[n - 1 = k(n - k^m)\] \[\begin{equation} \label{eq:3} n = \frac{k^{m+1}-1}{k-1} \end{equation}\]From \eqref{eq:3}
\(n > k^m\) \(\sqrt[m]{n} > k\)
From Binomial Thorem,
\[n = \sum_{i=0}^m{k}^i < (k+1)^m\]Therefore,
\[\begin{equation} \label{eq:4} k < \sqrt[m]{n} < k + 1 \end{equation}\] \[k = \left \lfloor{\sqrt[m]{n}}\right \rfloor\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public String smallestGoodBase(String n) {
long num = Long.valueOf(n);
BigInteger bn = BigInteger.valueOf(num);
// the smallest base is 2, so
// 2 <= m <= log_2^n
// if m == 1, then k == n - 1
int max = (int)(Math.log(num) / Math.log(2));
for (int m = max; m > 0; m--) {
// \sqrt[m]{n}
BigInteger k = BigInteger.valueOf((long) Math.floor(Math.pow(num, 1.0 / m)));
// k^(m + 1) - 1
BigInteger left = k.pow(m + 1).subtract(BigInteger.ONE);
// n(k - 1)
BigInteger right = bn.multiply(k.subtract(BigInteger.ONE));
if (left.equals(right)) {
return String.valueOf(k);
}
}
return String.valueOf(num - 1);
}
Dyanmical Systems
Attractor: a set of numerical values toward which a system tends to evolve, for a wide variety of starting conditions of the system.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public boolean isRobotBounded(String instructions) {
// N, E, S, W
int[][] directions = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int x = 0, y = 0, d = 0;
for (char c : instructions.toCharArray()) {
if (c == 'L') {
d = (d + 3) % 4;
} else if (c == 'R') {
d = (d + 1) % 4;
} else {
x += directions[d][0];
y += directions[d][1];
}
}
// after at most 4 cycles, the limit cycle trajectory returns to the initial point
return (x == 0 && y == 0) || d != 0;
}
Logarithm
1
2
3
4
public boolean isPowerOfThree(int n) {
// takes the decimal part
return (Math.log10(n) / Math.log10(3)) % 1 == 0;
}
Absolute Value
Maximum of Absolute Value Expression
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int maxAbsValExpr(int[] arr1, int[] arr2) {
int n = arr1.length;
// linear combinations
int[] c1 = new int[n], c2 = new int[n], c3 = new int[n], c4 = new int[n];
for (int i = 0; i < n; i++) {
c1[i] = arr1[i] + arr2[i] + i;
c2[i] = arr1[i] + arr2[i] - i;
c3[i] = arr1[i] - arr2[i] + i;
c4[i] = arr1[i] - arr2[i] - i;
}
int max = Integer.MIN_VALUE;
for (int[] c : new int[][]{c1, c2, c3, c4}) {
max = Math.max(max, maxDiff(c));
}
return max;
}
private int maxDiff(int[] c) {
Arrays.sort(c);
return c[c.length - 1] - c[0];
}
Reverse Subarray To Maximize Array Value
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public int maxValueAfterReverse(int[] nums) {
int n = nums.length;
int value = 0;
for (int i = 0; i < n - 1; i++) {
value += Math.abs(nums[i] - nums[i + 1]);
}
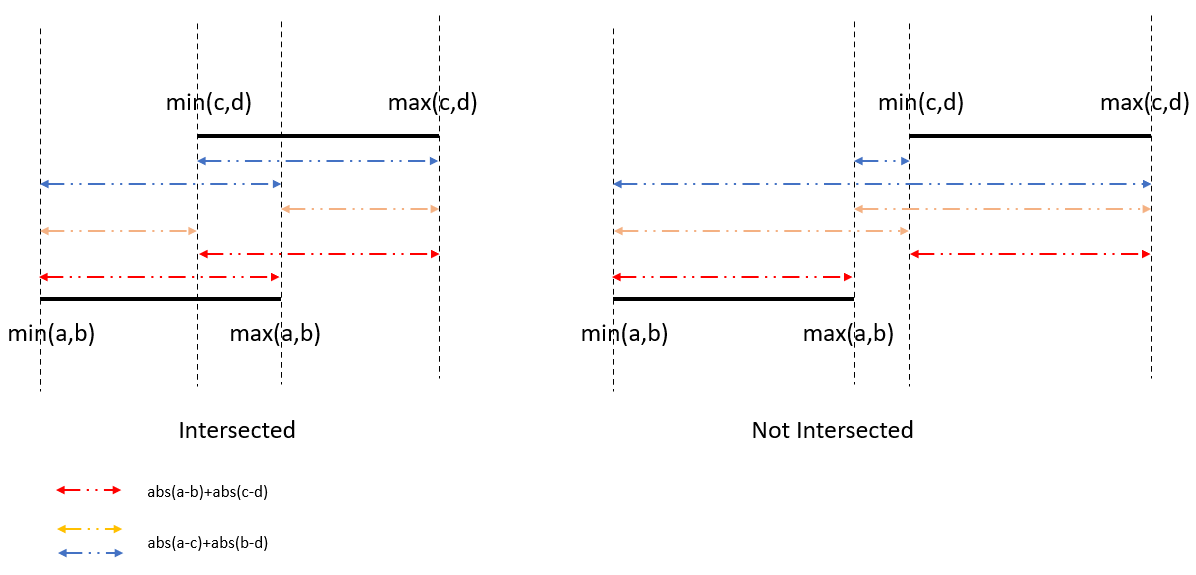
// ..., a, [b, ..., c], d, ...
// only if [min(a, b), max(a, b)] doesn't intersect with [min(c, d), max(c, d)]
// will the gain be positive
int low = Integer.MAX_VALUE, high = Integer.MIN_VALUE;
for (int i = 0; i < n - 1; i++) {
low = Math.min(low, Math.max(nums[i], nums[i + 1]));
high = Math.max(high, Math.min(nums[i], nums[i + 1]));
}
int gain = Math.max(0, (high - low) * 2);
// edge cases
for (int i = 1; i < n - 1; i++) {
// subarray starts at index 0
gain = Math.max(gain, Math.abs(nums[0] - nums[i + 1]) - Math.abs(nums[i] - nums[i + 1]));
// subarray ends at index n - 1
gain = Math.max(gain, Math.abs(nums[n - 1] - nums[i]) - Math.abs(nums[i + 1] - nums[i]));
}
return value + gain;
}
Minimax
Egg Drop With 2 Eggs and N Floors
1
2
3
4
5
6
7
8
9
10
public int twoEggDrop(int n) {
// minimax
//
// suppose the optimal answer is x,
// then the first number chosen cannot exceed x.
// the second guess cannot exceed (x - 1)
// ...
// 1 + 2 + ... + x >= n
return (int) Math.ceil((Math.sqrt(1 + 8 * n) - 1) / 2);
}
Another solution is recursion:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private int[][] memo;
public int twoEggDrop(int n) {
int eggs = 2;
this.memo = new int[n + 1][eggs + 1];
return drop(n, eggs);
}
private int drop(int n, int eggs) {
if (eggs == 1 || n <= 1) {
return n;
}
if (memo[n][eggs] > 0) {
return memo[n][eggs];
}
int min = n;
for (int i = 1; i <= n; i++) {
// break, not break
min = Math.min(min, 1 + Math.max(drop(i - 1, eggs - 1), drop(n - i, eggs)));
}
return memo[n][eggs] = min;
}
Generalization:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int superEggDrop(int k, int n) {
int low = 1, high = n;
while (low < high) {
int mid = (low + high) >>> 1;
if (f(mid, k, n) >= n) {
high = mid;
} else {
low = mid + 1;
}
}
return low;
}
// f(x) = sum_{i=1}^k{\binom{x}{i}}
public int f(int x, int k, int n) {
int sum = 0, c = 1;
for (int i = 1; i <= k && sum < n; i++) {
c *= x - i + 1;
c /= i;
sum += c;
}
return sum;
}
Dynamic Programming:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int superEggDrop(int k, int n) {
// dp[i][j]: max number of floor that we can test with i moves and j eggs
int[][] dp = new int[n + 1][k + 1];
int moves = 0;
while (dp[moves][k] < n) {
moves++;
for (int j = 1; j <= k; j++) {
// checks the floor dp[m - 1][j - 1] + 1
// if egg breaks, goes downstairs: 1 <= max floor <= dp[m - 1][j - 1]
// if egg doesn't break, goes upstairs: dp[m - 1][j - 1] + 2 <= max floor <= dp[m - 1][j - 1] + dp[m - 1][j] + 1
dp[moves][j] = 1 + dp[moves - 1][j - 1] + dp[moves - 1][j];
}
}
return moves;
}
Sequence
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int reachNumber(int target) {
// puts + and - signs on 1, 2, ..., k so that the sum == target
// symmetry
target = Math.abs(target);
int step = 0, sum = 0;
while (sum < target) {
step++;
sum += step;
}
// switching the sign of i will introduce a 2 * i delta
// so the delta must be even
while ((sum - target) % 2 != 0) {
step++;
sum += step;
}
return step;
}
Set Theory
Cantor’s diagonal argument: If s1, s2, … , sn, … is any enumeration of elements from T, then we can always construct an element s of T which doesn’t correspond to any sn in the enumeration.
1
2
3
4
5
6
7
public String findDifferentBinaryString(String[] nums) {
StringBuilder sb= new StringBuilder();
for (int i = 0; i < nums.length; i++) {
sb.append('1' - nums[i].charAt(i));
}
return sb.toString();
}
Dynamic Programming
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int numSquares(int n) {
vector<int> dp(n + 1, 1e4);
dp[0] = 0;
// Pre-calculates the square numbers
vector<int> squares(sqrt(n) + 1);
for (int i = 1; i < squares.size(); i++) {
squares[i] = i * i;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j < squares.size(); j++) {
if (i >= squares[j]) {
dp[i] = min(dp[i], dp[i - squares[j]] + 1);
}
}
}
return dp[n];
}