Knapsack Problem
Fundamentals
Backtracking takes \(O(2^n)\) time, so it’s less preferable. Dynamic Programming is better, and its form is like dp[i][j], which means the first i elements sums to j.
0-1 Knapsack Problem
maximize \(\sum _{i=1}^{n}v_{i}x_{i}\)
subject to \(\sum _{i=1}^{n}w_{i}x_{i}\leq W\) and \(x_{i}\in \{0,1\}\)
Template
Solving a Knapsack Problem effectively hinges on accurately defining three key components within the context of the specific problem and apply the template:
weight: the constrained resourcevalue: the benefit of selecting certain elementsf: the transition function, which dictates the optimal strategy for resource allocation.
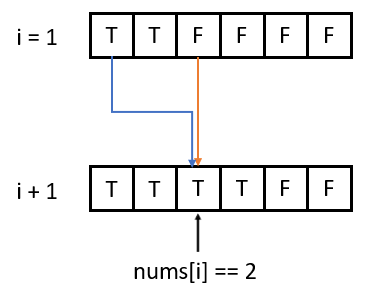
When the “weight” is an upper bound:
1
2
3
4
5
for (int elment : elements) {
for (int i = weight; i >= element; i--) {
dp[i] = f(dp[i], dp[i - element]);
}
}
The problem Parition Equal Subset Sum below demonstrates how the template is derived. Analogous to the Knapsack model: weight is the upper bound of the sum of the selected elements, and dp[i] is the optimal value when the weight sum is i.
The generalized form of the transition function f is dp = f(dp, pick current element, not pick current element). Its actual form depends on the problem. For example, in Parition Equal Subset Sum f is logical OR, while in Target Sum f is sum(). Sometimes the function can be complex, like that in Painting the Walls.
Remember the essence of the function is To pick, or not to pick.
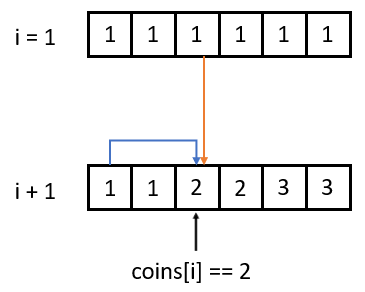
When the “weight” is a lower bound:
1
2
3
4
5
for (int elment : elements) {
for (int i = weight; i >= 0; i--) {
dp[i] = f(dp[i], dp[max(0, i - element)]);
}
}
See the example Profitable Schemes.
Find the Sum of the Power of All Subsequences
1
2
3
4
5
6
7
8
9
10
11
int sumOfPower(vector<int>& nums, int k) {
const int mod = 1e9 + 7;
vector<int> dp(k + 1);
dp[0] = 1;
for (const int& num : nums) {
for (int sum = k; sum >= 0; sum--) {
dp[sum] = (2ll * dp[sum] + (sum >= num ? dp[sum - num] : 0)) % mod;
}
}
return dp[k];
}
Subset Sum Problem
The subset sum problem (SSP): there is a multiset S of integers and a target-sum T, and the question is to decide whether any subset of the integers sum to precisely T. It’s NP-complete.
With full dimensionality (no reduction), we can backtrace.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public boolean canPartition(int[] nums) {
int n = nums.length, sum = Arrays.stream(nums).sum();
if (sum % 2 == 1) {
return false;
}
// dp[i][j]: whether the first i elements can sum up to j
boolean[][] dp = new boolean[n + 1][sum / 2 + 1];
dp[0][0] = true;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= sum / 2; j++) {
if (j < nums[i]) {
dp[i + 1][j] = dp[i][j];
} else {
// no picks || picks nums[i]
dp[i + 1][j] = dp[i][j] || dp[i][j - nums[i]];
}
}
}
return dp[n][sum / 2];
}
For example, nums = [1,2,5,1], then dp is:
1
2
3
4
5
[true,false,false,false,false,false]
[true,true,false,false,false,false]
[true,true,true,true,false,false]
[true,true,true,true,false,true]
[true,true,true,true,true,true]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if (sum % 2 == 1) {
return false;
}
boolean[] dp = new boolean[sum / 2 + 1];
dp[0] = true;
for (int num : nums) {
// dp[k + 1][i] depends on dp[k][i - num]
// so the iteration order is reversed
for (int i = sum / 2; i >= num; i--) {
dp[i] = dp[i] || dp[i - num];
}
}
return dp[sum / 2];
}
In 2D, dp[i + 1][j] = dp[i][j] || dp[i][j - nums[i]]. The reverse iteration ensures dp[i][j - nums[i]] is not updated to dp[i + 1][j - nums[i]] before we update dp[i][j] to dp[i + 1][j].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int findTargetSumWays(int[] nums, int target) {
int sum = Arrays.stream(nums).sum();
// sum(P) - sum(N) == target
// sum(P) - (sum - sum(P)) == target
// 2 * sum(P) == target + sum
// sum(P) == (target + sum) / 2
return target + sum < 0 || (target + sum) % 2 > 0 ? 0 : subsetSum(nums, (target + sum) >>> 1);
}
private int subsetSum(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = target; i >= num; i--) {
dp[i] += dp[i - num];
}
}
return dp[target];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
private static final int MOD = (int)1e9 + 7;
public int countPartitions(int[] nums, int k) {
long sum = 0, count = 1;
long[] dp = new long[k];
dp[0] = 1;
for (int num : nums) {
for (int i = k - 1; i >= num; i--) {
dp[i] = (dp[i] + dp[i - num]) % MOD;
}
count = count * 2 % MOD;
sum += num;
}
// now count == 2 ^ n is the total number of distinct partitions
for (int i = 0; i < k; i++) {
// sa = sum(group_a) = i
// sb = sum(group_b) = sum - i
//
// inclusion–exclusion principle
// set A: sa < k
// set B: sb < k
// set A and B (intersection): sa < k && sb < k
// set A or B (union): total count
//
// if only one of the groups has sum < k, say sa = i < k
// its inverse pair (sa = sum - i, sb = i) also needs to be deducted from total
// so count -= 2 * dp[i]
//
// if both groups have sum < k, i.e. sa = i < k, sb = sum - i < k
// it's the intersection, so count -= dp[i]
count -= dp[i] * (sum - i < k ? 1 : 2);
}
return (int)((count % MOD + MOD) % MOD);
}
Transition Functions
Max
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int lastStoneWeightII(int[] stones) {
int sum = Arrays.stream(stones).sum();
// dp[i]: weight sum of stones that is closest to i
// it's possible that no group of stones can sum to i
// e.g. stones = [1,2,5]
// dp = [0, 1, 2, 3, 3]
// dp[sum / 2] = dp[4] = 3, i.e. stone 1 and 2
int[] dp = new int[sum / 2 + 1];
for (int stone : stones) {
// the smaller group has a sum no greater than sum / 2
for (int i = sum / 2; i >= stone; i--) {
dp[i] = Math.max(dp[i], dp[i - stone] + stone);
}
}
return sum - 2 * dp[sum / 2];
}
Another solution is subset sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int lastStoneWeightII(int[] stones) {
int sum = Arrays.stream(stones).sum();
boolean[] dp = new boolean[sum / 2 + 1];
dp[0] = true;
for (int stone : stones) {
// considers smaller group only
for (int i = sum / 2; i >= stone; i--) {
dp[i] = dp[i] || dp[i - stone];
}
}
// smaller group
for (int i = sum / 2; i >= 0; i--) {
if (dp[i]) {
return sum - 2 * i;
}
}
return 0;
}
Maximum Profit From Trading Stocks
1
2
3
4
5
6
7
8
9
public int maximumProfit(int[] present, int[] future, int budget) {
int[] dp = new int[budget + 1];
for (int i = 0; i < present.length; i++) {
for (int j = budget; j >= present[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - present[i]] + future[i] - present[i]);
}
}
return dp[budget];
}
Probability
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public double probabilityOfHeads(double[] prob, int target) {
int n = prob.length;
// dp[i][j]: probability that the number of the first i coins equals j
double[][] dp = new double[n + 1][target + 1];
dp[0][0] = 1d;
for (int i = 0; i < n; i++) {
dp[i + 1][0] = dp[i][0] * (1 - prob[i]);
}
for (int i = 0; i < n; i++) {
for (int j = 1; j <= target; j++) {
dp[i + 1][j] = dp[i][j] * (1 - prob[i]) + dp[i][j - 1] * prob[i];
}
}
return dp[n][target];
}
Multi-dimension
Imagine the constraint of each item is not only a one-dimensional “weight” - instead, it’s a two-dimensional height and width constraint.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length;
int[][][] dp = new int[len + 1][m + 1][n + 1];
for (int i = 0; i < len; i++) {
int zeroes = (int)strs[i].chars().filter(ch -> ch == '0').count();
int ones = strs[i].length() - zeroes;
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (j < zeroes || k < ones) {
dp[i + 1][j][k] = dp[i][j][k];
} else {
dp[i + 1][j][k] = Math.max(dp[i][j][k], dp[i][j - zeroes][k - ones] + 1);
}
}
}
}
return dp[len][m][n];
}
2D:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (String str : strs) {
int zeroes = (int)str.chars().filter(ch -> ch == '0').count();
int ones = str.length() - zeroes;
for (int i = m; i >= zeroes; i--) {
for (int j = n; j >= ones; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeroes][j - ones] + 1);
}
}
}
return dp[m][n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
const int mod = 1e9 + 7;
// dp[i][j]: count of schemes with profit >= j done by exactly i members
vector<vector<int>> dp(n + 1, vector<int>(minProfit + 1));
dp[0][0] = 1;
for (int k = 0; k < group.size(); k++) {
for (int i = n; i >= group[k]; i--) {
for (int j = minProfit; j >= 0; j--) {
dp[i][j] = (dp[i][j] + dp[i - group[k]][max(0, j - profit[k])]) % mod;
}
}
}
return accumulate(dp.begin(), dp.end(), 0,
[minProfit, mod](int acc, const vector<int>& vec) {
return (acc + vec[minProfit]) % mod;
});
}
Multiset
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private static final int MOD = (int)1e9 + 7;
public int waysToReachTarget(int target, int[][] types) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int[] t : types) {
for (int j = target; j > 0; j--) {
for (int k = 1; k <= t[0] && k * t[1] <= j; k++) {
dp[j] = (dp[j] + dp[j - k * t[1]]) % MOD;
}
}
}
return dp[target];
}
Count of Sub-Multisets With Bounded Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int countSubMultisets(vector<int>& nums, int l, int r) {
unordered_map<int, int> freqs;
for (int num : nums) {
freqs[num]++;
}
const int mod = 1e9 + 7;
vector<int> dp(r + 1);
dp[0] = 1;
// Knapsack
for (const auto& [num, f] : freqs) {
// Compute from dp[0] to dp[r]
for (int t = r; t > max(0, r - num); t--) {
long v = 0;
// v = dp[t] + dp[t - num] + dp[t - 2 * num] + ... + dp[t - c * num]
// where c < f and c is the greatest number that satisfies t - c * m >= 0
for (int k = 0; k < f && k * num <= t; k++) {
v += dp[t - k * num];
}
// Sliding window to reduce repeated computation
// Compute dp[t], dp[t - num], dp[t - 2 * num], ...
// dp[t] += dp[t - num] + dp[t - 2 * num] + ... + dp[t - c * num]
// = v - dp[t]
for (int j = t; j > 0; j -= num) {
v = (v - dp[j] + mod) % mod;
if (f * num <= j) {
v = (v + dp[j - f * num]) % mod;
}
dp[j] = (dp[j] + v) % mod;
}
}
}
// Each sub-multiset can be padded with m zeros, where m \in [0, freqs[0]]
// Therefore, the multiplier is (freqs[0] + 1)
return (freqs[0] + 1) * accumulate(dp.begin() + l, dp.begin() + r + 1, 0ll, [&](int a, int b){ return (a + b) % mod; }) % mod;
}
Count of Selected Elements
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public boolean splitArraySameAverage(int[] nums) {
int n = nums.length, sum = Arrays.stream(nums).sum();
// assumes size(A) <= size(B)
// dp[i][j]: whether it's possible to sum to i with j elements in array A
boolean[][] dp = new boolean[sum + 1][n / 2 + 1];
dp[0][0] = true;
for (int num : nums) {
for (int i = sum; i >= num; i--) {
// the second dimension is used to record the count of selected elements
for (int j = 1; j <= n / 2; j++) {
dp[i][j] = dp[i][j] || dp[i - num][j - 1];
}
}
}
// when avg(A) == avg(B) == avg(nums)
// sum(A) = avg(nums) * size(A)
// = sum * size(A) / n
// iterates size(A) from 1 through n / 2
for (int i = 1; i <= n / 2; i++) {
if (sum * i % n == 0 && dp[sum * i / n][i]) {
return true;
}
}
return false;
}
Dependency
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private static final int MAX_COST = (int)5e8;
public int paintWalls(int[] cost, int[] time) {
int n = cost.length;
// dp[i]: min amount of money required to paint i walls
int[] dp = new int[n + 1];
Arrays.fill(dp, MAX_COST);
dp[0] = 0;
for (int i = 0; i < n; i++) {
// j is the number of remaining walls
for (int j = n; j > 0; j--) {
// If a paid painter is selected for the current wall,
// then in the time period time[i]:
// * 1 wall is painted by the paid painter
// * at most time[i] walls are painted by free painter
dp[j] = Math.min(dp[j], dp[Math.max(j - time[i] - 1, 0)] + cost[i]);
}
}
return dp[n];
}
Top-down
Maximize Total Tastiness of Purchased Fruits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
private int[] price, tastiness;
private int maxAmount, maxCoupons;
private Integer[][][] memo;
public int maxTastiness(int[] price, int[] tastiness, int maxAmount, int maxCoupons) {
this.price = price;
this.tastiness = tastiness;
this.maxAmount = maxAmount;
this.maxCoupons = maxCoupons;
this.memo = new Integer[price.length + 1][maxAmount + 1][maxCoupons + 1];
return dfs(0, maxAmount, maxCoupons);
}
private int dfs(int i, int amount, int coupon) {
if (i == price.length) {
return 0;
}
if (memo[i][amount][coupon] != null) {
return memo[i][amount][coupon];
}
int max = dfs(i + 1, amount, coupon);
if (price[i] <= amount) {
max = Math.max(max, dfs(i + 1, amount - price[i], coupon) + tastiness[i]);
}
if (coupon > 0 && price[i] / 2 <= amount) {
max = Math.max(max, dfs(i + 1, amount - price[i] / 2, coupon - 1) + tastiness[i]);
}
return memo[i][amount][coupon] = max;
}
Unbounded Knapsack Problem (UKP)
maximize \(\sum _{i=1}^{n}v_{i}x_{i}\)
subject to \(\sum _{i=1}^{n}w_{i}x_{i}\leq W\) and \(x_{i}\geq 0,\ x_{i}\in \mathbb {Z}\)
Change-making Problem
Change-making problem: Weakly NP-hard. Find the minimum number of coins (of certain denominations) that add up to a given amount of money. It is a special case of the integer knapsack problem.
minimize \(f(W)=\sum _{j=1}^{n}x_{j}\)
subject to \(\sum _{j=1}^{n}w_{j}x_{j}=W\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int coinChange(int[] coins, int amount) {
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
for (int i = 0; i < dp.length; i++) {
Arrays.fill(dp[i], amount + 1);
}
for (int i = 0; i < dp.length; i++) {
dp[i][0] = 0;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j <= amount; j++) {
if (j < coins[i]) {
dp[i + 1][j] = dp[i][j];
} else {
dp[i + 1][j] = Math.min(dp[i][j], dp[i + 1][j - coins[i]] + 1);
}
}
}
return dp[n][amount] > amount ? -1 : dp[n][amount];
}
1
2
3
4
5
6
7
8
9
10
11
12
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int change(int amount, int[] coins) {
int n = coins.length;
// dp[i][j]: combinations to make up amount j by using the first i kinds of coins
int[][] dp = new int[n + 2][amount + 1];
dp[0][0] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= amount; j++) {
if (j < coins[i]) {
dp[i + 1][j] = dp[i][j];
} else {
dp[i + 1][j] = dp[i][j] + dp[i + 1][j - coins[i]];
}
}
}
return dp[n][amount];
}
For example, amount = 5, coins = [1, 2, 5], then dp is:
1
2
3
4
[1,0,0,0,0,0]
[1,1,1,1,1,1]
[1,1,2,2,3,3]
[1,1,2,2,3,4]
1
2
3
4
5
6
7
8
9
10
11
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
In 2D, dp[i + 1][j] = dp[i][j] + dp[i + 1][j - nums[i]]. The natural iteration ensures dp[i][j - nums[i]] is updated to dp[i + 1][j - nums[i]] before we update dp[i][j] to dp[i + 1][j].
Number of Ways to Build House of Cards
1
2
3
4
5
6
7
8
9
10
11
12
public int houseOfCards(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
// it takes 2 * k - 1 cards to build a row
// 2, 5, 8, ...
for (int cards = 2; cards <= n; cards += 3) {
for (int i = n; i >= cards; i--) {
dp[i] += dp[i - cards];
}
}
return dp[n];
}
Form Largest Integer With Digits That Add up to Target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public String largestNumber(int[] cost, int target) {
int n = 9;
String[][] dp = new String[n + 1][target + 1];
dp[0][0] = "";
for (int i = 0; i < n; i++) {
for (int j = 0; j <= target; j++) {
if (j < cost[i] || dp[i + 1][j - cost[i]] == null) {
dp[i + 1][j] = dp[i][j];
} else {
// i is increasing, and that ensures (i + 1) + dp[i + 1][j - cost[i]] is always the largest
// among all possible combinations with the same set of digits
// therefore, no sorting is required
dp[i + 1][j] = max(dp[i][j], (i + 1) + dp[i + 1][j - cost[i]]);
}
}
}
return dp[n][target] == null ? "0" : dp[n][target];
}
private String max(String a, String b) {
return a == null ? b : (a.length() == b.length() ?
(a.compareTo(b) > 0 ? a : b) :
(a.length() > b.length() ? a : b));
}
Permutation Sum
The below permutation sum (yes it’s permutation, ignore the wrong problem name) is not a knapsack problem, but the only difference is the loop order:
1
2
3
4
5
6
7
8
9
10
11
12
13
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 0; i <= target; i++) {
for (int num : nums) {
if (i >= num) {
dp[i] += dp[i - num];
}
}
}
return dp[target];
}
In essence, it’s bottom-up DP.
Similar problem: Count Ways To Build Good Strings
1
2
3
4
5
6
7
8
9
10
11
int sum = 0;
for (int i = 0; i <= high; i++) {
for (int num : new int[]{zero, one}) {
if (i >= num) {
dp[i] = (dp[i] + dp[i - num]) % MOD;
}
}
if (i >= low) {
sum = (sum + dp[i]) % MOD;
}
}
Even if zero and one are equal, they represent different base values. This is a bit different from the requirement of Combination Sum IV that all base numbers are distinct.
Summary
| 2D | 1D order | |
|---|---|---|
| 0-1 | dp[i + 1][j] = dp[i][j] + dp[i][j - num] | j: num <- target (decreasing) |
| UKP | dp[i + 1][j] = dp[i][j] + dp[i + 1][j - num] | j: num -> target (increasing) |