Frog Jump II
1
2
3
4
5
6
7
8
9
10
| public int maxJump(int[] stones) {
// it's optimal to use of all rocks
// it's not optimal to use two consecutive rocks
// because on the way back, stones[i + 2] - stones[i] > stones[i + 1] - stones[i]
int cost = stones[1] - stones[0], n = stones.length;
for (int i = 2; i < n; i++) {
cost = Math.max(cost, stones[i] - stones[i - 2]);
}
return cost;
}
|
Partition String Into Substrings With Values at Most K
Flower Planting With No Adjacent
No node has more than 3 neighbors, so there’s always one possible color to pick.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| private final int numFlowers = 4;
public int[] gardenNoAdj(int N, int[][] paths) {
// constructs the graph
Map<Integer, List<Integer>> graph = new HashMap<>();
for (int i = 1; i <= N; i++) {
graph.put(i, new ArrayList<>());
}
for (int[] p : paths) {
graph.get(p[0]).add(p[1]);
graph.get(p[1]).add(p[0]);
}
int[] result = new int[N];
for (int i = 1; i <= N; i++) {
// flowers[i] indicates whether the (i + 1)th flower has been picked
boolean[] flowers = new boolean[numFlowers];
// finds the neighbors who have picked a flower
for (int garden : graph.get(i)) {
if (result[garden - 1] > 0) {
flowers[result[garden - 1] - 1] = true;
}
}
// picks the first available flower
for (int f = 1; f <= numFlowers; f++) {
if (!flowers[f - 1]) {
result[i - 1] = f;
break;
}
}
}
return result;
}
|
Jump Game
1
2
3
4
5
6
7
| public boolean canJump(int[] nums) {
int i = 0;
for (int reach = 0; i <= reach && i < nums.length; i++) {
reach = Math.max(reach, i + nums[i]);
}
return i == nums.length;
}
|
Video Stitching
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int videoStitching(int[][] clips, int T) {
Arrays.sort(clips, (a, b) -> a[0] - b[0]);
int i = 0, start = 0, end = 0, result = 0;
while (start < T) {
while (i < clips.length && clips[i][0] <= start) {
end = Math.max(end, clips[i++][1]);
}
if (start == end) {
return -1;
}
start = end;
result++;
}
return result;
}
|
Broken Calculator
1
2
3
4
5
6
7
8
| public int brokenCalc(int startValue, int target) {
int s = 0;
while (target > startValue) {
target = target % 2 == 0 ? target / 2 : target + 1;
s++;
}
return s + startValue - target;
}
|
Split Array into Consecutive Subsequences
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public boolean isPossible(int[] nums) {
int prev = Integer.MIN_VALUE, curr = 0;
// count of consecutive subsequences with size i, ending at prev/curr
int p1 = 0, p2 = 0, p3 = 0;
int c1 = 1, c2 = 0, c3 = 0;
for (int i = 0; i < nums.length; prev = curr, p1 = c1, p2 = c2, p3 = c3) {
int count = 0;
for (curr = nums[i]; i < nums.length && curr == nums[i]; i++) {
count++;
}
// fills the sets greedily: 1 -> 2 -> 3
if (curr != prev + 1) {
if (p1 != 0 || p2 != 0) {
return false;
}
c1 = count;
c2 = 0;
c3 = 0;
} else {
if (count < p1 + p2) {
return false;
}
c1 = Math.max(0, count - (p1 + p2 + p3));
c2 = p1;
c3 = p2 + Math.min(p3, count - (p1 + p2));
}
}
return p1 == 0 && p2 == 0;
}
|
Hand of Straights
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public boolean isNStraightHand(int[] hand, int W) {
Map<Integer, Integer> count = new TreeMap<>();
for (int h : hand) {
count.put(h, count.getOrDefault(h, 0) + 1);
}
// number of groups that are not closed
int prev = -1, opened = 0;
// The i-th queue element is the number of opened groups starting from the i-th key
Queue<Integer> q = new LinkedList<>();
for (var e : count.entrySet()) {
int k = e.getKey(), v = e.getValue();
if ((opened > 0 && k > prev + 1) || opened > v) {
return false;
}
q.add(v - opened);
prev = k;
opened = v;
if (q.size() == W) {
opened -= q.poll();
}
}
return opened == 0;
}
|
Wiggle Sort
1
2
3
4
5
6
7
8
9
10
11
12
13
| public void wiggleSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
if ((i % 2 == 0) == (nums[i] > nums[i + 1])) {
swap(nums, i, i + 1);
}
}
}
private void swap(int[] A, int i, int j) {
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
|
Minimum Factorization
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int smallestFactorization(int a) {
if (a < 10) {
return a;
}
long b = 0, t = 1;
for (int i = 9; i >= 2; i--) {
while (a % i == 0) {
a /= i;
b += t * i;
t *= 10;
}
}
return a == 1 && b <= Integer.MAX_VALUE ? (int)b : 0;
}
|
Put Boxes Into the Warehouse I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public int maxBoxesInWarehouse(int[] boxes, int[] warehouse) {
Arrays.sort(boxes);
int i = boxes.length - 1, j = 0, count = 0;
while (i >= 0 && j < warehouse.length) {
// all following boxes will fit in warehouse[j]
if (boxes[i] <= warehouse[j]) {
j++;
count++;
}
i--;
}
return count;
}
|
Maximum Binary String After Change
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public String maximumBinaryString(String binary) {
// we can always make the string contain at most one '0'
int ones = 0, zeros = 0, n = binary.length();
StringBuilder sb = new StringBuilder("1".repeat(n));
for (int i = 0; i < n; i++) {
if (binary.charAt(i) == '0') {
zeros++;
} else if (zeros == 0) {
// leading '1's
ones++;
}
}
if (ones < n) {
sb.setCharAt(ones + zeros - 1, '0');
}
return sb.toString();
}
|
Maximum Number of Ones
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public int maximumNumberOfOnes(int width, int height, int sideLength, int maxOnes) {
// greedy - translation of a single sub-matrix
// considers all positions in the sub-matrix
// counts their occurrences in M
int[] count = new int[sideLength * sideLength];
for (int i = 0; i < sideLength; i++) {
for (int j = 0; j < sideLength; j++) {
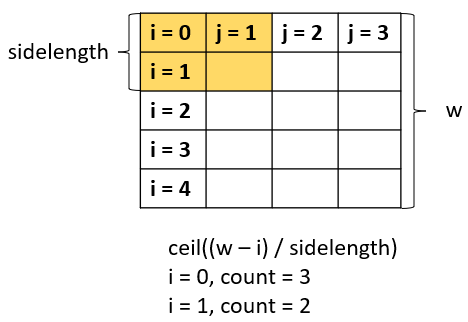
// Math.ceil((width - i) / (double)sideLength)
count[i * sideLength + j] += ((width - i - 1) / sideLength + 1) * ((height - j - 1) / sideLength + 1);
}
}
// sorts the positions by occurrences
Arrays.sort(count);
// assigns ones to positions with more occurrences
int sum = 0;
for (int i = count.length - 1; i > count.length - 1 - maxOnes; i--) {
sum += count[i];
}
return sum;
}
|
Strong Password Checker
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| public int strongPasswordChecker(String s) {
int missingTypes = 3;
for (char c : s.toCharArray()) {
if (Character.isUpperCase(c)) {
missingTypes--;
break;
}
}
for (char c : s.toCharArray()) {
if (Character.isLowerCase(c)) {
missingTypes--;
break;
}
}
for (char c : s.toCharArray()) {
if (Character.isDigit(c)) {
missingTypes--;
break;
}
}
int n = s.length();
if (n < 6) {
// (6 - n): number of chars to be inserted
// if 6 - n < missingTypes, we will need to replace some chars, too
// the length of a repeating char seq <= 5
// so one insertion can break it
return Math.max(6 - n, missingTypes);
}
// mod0: count of repeating char seq those length % 3 == 0
// mod1: count of repeating char seq those length % 3 == 1
int i = 2, mod0 = 0, mod1 = 0, replacements = 0;
while (i < n) {
// three repeating chars in a row
if (s.charAt(i) == s.charAt(i - 1) && s.charAt(i) == s.charAt(i - 2)) {
// finds the length of the sequence
int len = 2;
while (i < n && s.charAt(i) == s.charAt(i - 1)) {
len++;
i++;
}
// always replace the third char
replacements += len / 3;
if (len % 3 == 0) {
mod0++;
} else if (len % 3 == 1) {
mod1++;
}
} else {
i++;
}
}
if (n <= 20) {
// minimum replacement
return Math.max(replacements, missingTypes);
}
// when n > 20, the idea is to prefer deletions over replacements
// (length / 3) replacements = (length / 3 - 1) replacements + (length % 3 + 1) deletions
int deletes = n - 20;
// length % 3 == 0, one replacement => one deletion
replacements -= Math.min(mod0, deletes);
// length % 3 == 1, one replacement => two deletions
// Math.max(deletes - mod0, 0) is the remaining deletes after the above action
replacements -= Math.min(Math.max(deletes - mod0, 0), mod1 * 2) / 2;
// length % 3 == 2, one replacement => three deletions
// Math.max(deletes - mod0 - mod1 * 2, 0) is the remaining deletes after the above actions
replacements -= Math.max(deletes - mod0 - mod1 * 2, 0) / 3;
return deletes + Math.max(replacements, missingTypes);
}
|
Minimum Adjacent Swaps to Reach the Kth Smallest Number
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int getMinSwaps(String num, int k) {
char[] chars = num.toCharArray();
for (int i = 0; i < k; i++) {
nextPermutation(chars);
}
int n = num.length(), count = 0;
for (int i = 0; i < n; i++) {
if (num.charAt(i) != chars[i]) {
for (int j = i + 1; j < n; j++) {
swap(chars, i, j);
count++;
if (num.charAt(i) == chars[i]) {
break;
}
}
}
}
return count;
}
|
Minimum Initial Energy to Finish Tasks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int minimumEffort(int[][] tasks) {
// sorts to maximize running energy
Arrays.sort(tasks, Comparator.comparingInt(a -> a[0] - a[1]));
int initial = 0, energy = 0;
for (int[] t : tasks) {
if (energy < t[1]) {
initial += t[1] - energy;
energy = t[1] - t[0];
} else {
energy -= t[0];
}
}
return initial;
}
|
Minimum Number of Days to Eat N Oranges
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| private Map<Integer, Integer> memo = new HashMap<>();
public int minDays(int n) {
if (n < 2) {
return n;
}
if (memo.containsKey(n)) {
return memo.get(n);
}
int days = 1 + Math.min(n % 2 + minDays(n / 2), n % 3 + minDays(n / 3));
memo.put(n, days);
return days;
}
|
Minimum Number of People to Teach
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| public int minimumTeachings(int n, int[][] languages, int[][] friendships) {
int m = languages.length;
// language set for each user
Set<Integer>[] ls = new Set[m + 1];
for (int i = 1; i <= m; i++) {
ls[i] = new HashSet<>();
}
for (int i = 0; i < m; i++) {
ls[i + 1] = Arrays.stream(languages[i]).boxed().collect(Collectors.toSet());
}
// finds the set of people who can't communicate with at least one friend
Set<Integer> set = new HashSet<>();
for (int[] f : friendships) {
if (Collections.disjoint(ls[f[0]], ls[f[1]])) {
set.add(f[0]);
set.add(f[1]);
}
}
// finds the count of users in the set that speak each language
int[] userCount = new int[n + 1];
for (int u : set) {
for (int l : languages[u - 1]) {
userCount[l]++;
}
}
// finds the language that most people know
return set.size() - Arrays.stream(userCount).max().getAsInt();
}
|
Maximum Score From Removing Substrings
1
2
3
4
5
6
| public int maximumGain(String s, int x, int y) {
StringBuilder sb = new StringBuilder(s);
// greedily removes the pattern with greater points, then remove the other pattern
// intuition: the total number of deletions is a fixed value, no matter which pattern is deleted first
return x > y ? remove(sb, "ab", x) + remove(sb, "ba", y) : remove(sb, "ba", y) + remove(sb, "ab", x);
}
|
Earliest Possible Day of Full Bloom
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int earliestFullBloom(int[] plantTime, int[] growTime) {
int n = plantTime.length;
Integer[] index = new Integer[n];
for (int i = 0; i < n; i++) {
index[i] = i;
}
// switching between seeds just delays the starting grow time for (at least one of) the seeds
// so we never switch
// plants seeds with greater growTime first
Arrays.sort(index, Comparator.comparingInt(i -> -growTime[i]));
int start = 0, end = 0;
for (int i : index) {
end = Math.max(end, start + plantTime[i] + growTime[i]);
start += plantTime[i];
}
return end;
}
|
Make Array Non-decreasing or Non-increasing
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public int convertArray(int[] nums) {
return Math.min(helper(nums, 1), helper(nums, -1));
}
private int helper(int[] nums, int sign) {
Queue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());
int cost = 0;
for (int i = sign > 0 ? 0 : nums.length - 1; i < nums.length && i >= 0; i += sign) {
if (!pq.isEmpty() && pq.peek() > nums[i]) {
cost += pq.poll() - nums[i];
pq.offer(nums[i]);
}
pq.offer(nums[i]);
}
return cost;
}
|
Minimum Operations to Form Subsequence With Target Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| int minOperations(vector<int>& nums, int target) {
long long sum = accumulate(nums.begin(), nums.end(), 0l);
if (sum < target) {
return -1;
}
sort(nums.begin(), nums.end());
int ops = 0;
while (target > 0) {
int mx = nums.back();
nums.pop_back();
if (sum - mx >= target) {
// All the elements other than max can sum to target
// so it's safe to skip mx directly
sum -= mx;
} else if (mx <= target) {
// Picks the current max
sum -= mx;
target -= mx;
} else {
// sum - mx < target && mx > target
// sum < mx + target < 2 * mx
// mx > sum / 2
nums.push_back(mx / 2);
nums.push_back(mx / 2);
ops++;
}
}
return ops;
}
|