Graph Cycle

Acyclic Graph

flowchart LR
    A([Acyclic Graph]) --> B{Directed?}
    B -->|Yes| C[DAG]
    B -->|No| D{Forest}
    D --> E{Connected?}
    E -->|Yes| F{Tree}

A topological sorting is possible iff the graph is a DAG.

Cyclic Graph

Common graph cycle problems:

• Cycle detection
• Cycle length

Khan’s Algorithm

See Topological Sorting

A directed graph with n nodes and n edges. Each node has one and only one outgoing edge. Loops are not allowed.

Maximum Employees to Be Invited to a Meeting

public int maximumInvitations(int[] favorite) {
    int n = favorite.length;
    // Constucts a graph by creating a directed edge i -> favorite[i] for each node
    //
    // The graph has possibly more than one component.
    // Each component is a cycle (length > 1); each node on the cycle can have an "arm" (acyclic nodes)

    // Kahn's Algorithm picks out acyclic nodes
    int[] indegrees = new int[n];
    for (int i = 0; i < n; i++) {
        indegrees[favorite[i]]++;
    }

    // Enqueues leaves
    Queue<Integer> q = new LinkedList<>();
    boolean[] visited = new boolean[n];
    for (int i = 0; i < n; i++) {
        if (indegrees[i] == 0) {
            visited[i] = true;
            q.offer(i);
        }
    }

    // dp[i]: longest path from leaves to i exclusively
    int[] dp = new int[n]; 
    while (!q.isEmpty()) {
        int node = q.poll(), to = favorite[node];
        dp[to] = Math.max(dp[to], dp[node] + 1);

        if (--indegrees[to] == 0) {
            visited[to] = true;
            q.offer(to);
        }
    }

    int count1 = 0;  // case 1: cycle length == 2
    int count2 = 0;  // case 2: cycle length > 2
    for (int i = 0; i < n; i++) {
        if (!visited[i]) {
            // Gets the cycle length
            int length = 0;
            for (int j = i; !visited[j]; j = favorite[j]) {
                visited[j] = true;
                length++;
            }

            if (length == 2) {  // Case 1
                // The max path of each component is (2 + lengths of the two arms)
                // We can put the max paths of all the components along the circular table,
                // side by side.
                count1 += 2 + dp[i] + dp[favorite[i]];
            } else {  // Case 2
                // Only the on-cycle nodes can be seated on the table
                // Arms can't be seated
                count2 = Math.max(count2, length);
            }
        }
    }
    return Math.max(count1, count2);
}

White-Gray-Black DFS

Course Schedule II

private List<Integer>[] graph;
private Color[] color;
private List<Integer> order = new ArrayList<>();

private enum Color {
    WHITE,  // node is not processed yet
    GRAY,  // node is being processed
    BLACK  // node and all its descendants are processed
}

public int[] findOrder(int numCourses, int[][] prerequisites) {
    color = new Color[numCourses];

    // by default all nodes are WHITE
    Arrays.fill(color, Color.WHITE);

    graph = new List[numCourses];
    for (int i = 0; i < numCourses; i++) {
        graph[i] = new ArrayList<>();
    }
    for (int[] p : prerequisites) {
        graph[p[1]].add(p[0]);
    }

    // dfs unprocessed node
    for (int i = 0; i < numCourses; i++) {
        if (color[i] == Color.WHITE) {
            if (!dfs(i)) {
                return new int[0];
            }
        }
    }

    Collections.reverse(order);
    return order.stream().mapToInt(Integer::valueOf).toArray();
}

// returns false if cycle is detected.
private boolean dfs(int node) {
    // starts the recursion
    color[node] = Color.GRAY;

    for (int neighbor : graph[node]) {
        // skips back nodes
        // stops if cycle detected
        if ((color[neighbor] == Color.WHITE && !dfs(neighbor)) || color[neighbor] == Color.GRAY) {
            return false;
        }
    }

    // finishes the recursion
    color[node] = Color.BLACK;
    order.add(node);
    return true;
}

Similar problem in grid: Detect Cycles in 2D Grid

To complete DFS in grid to simulate directed graph, in each DFS path we don’t visit the prev visited cell.

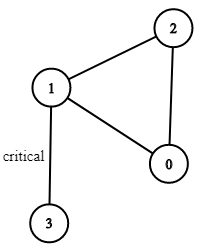
Critical Connections in a Network

private List<List<Integer>> graph;
private Set<List<Integer>> set;

public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
    this.graph = new ArrayList<>(n);
    for (int i = 0; i < n; i++) {
        graph.add(new ArrayList<>());
    }
    for (List<Integer> e : connections) {
        int s1 = e.get(0), s2 = e.get(1);
        graph.get(s1).add(s2);
        graph.get(s2).add(s1);
    }

    this.set = new HashSet<>(connections);

    // the depth of a node during DFS
    int[] rank = new int[n];
    Arrays.fill(rank, -2);

    dfs(rank, 0, 0);
    return new ArrayList<>(set);
}

// returns min depth of all nodes in the subtree
private int dfs(int[] rank, int node, int depth) {
    if (rank[node] >= 0) {
        return rank[node];
    }

    rank[node] = depth;

    int min = depth;
    for (int neighbor: graph.get(node)) {
        // skips parent
        // here's the reason why rank is initialized with -2, rather than -1:
        // if depth == 0, then its child node will be skipped by mistake
        if (rank[neighbor] == depth - 1) {
            continue;
        }

        int minSub = dfs(rank, neighbor, depth + 1);
        min = Math.min(min, minSub);

        // cycle detected
        if (minSub <= depth) {
            // discards the edge (node, neighbor) in the cycle
            set.remove(Arrays.asList(node, neighbor));
            set.remove(Arrays.asList(neighbor, node));
        }
    }
    return min;
}

This algorithm is very similar to Tarjan’s Algorithm. The meaning of rank and dfn/low is slightly different, but in essence they are closely related.

node: 0
rank: 0,-2,-2,-2

node: 1
rank: 0,1,-2,-2

node: 2
rank: 0,1,2,-2

neighbor: 0
depth: 2
minSub: 0
rank: 0,1,2,-2

neighbor: 2
depth: 1
minSub: 0
rank: 0,1,2,-2

node: 3
rank: 0,1,2,2

neighbor: 3
depth: 1
minSub: 2
rank: 0,1,2,2

neighbor: 1
depth: 0
minSub: 0
rank: 0,1,2,2

neighbor: 2
depth: 0
minSub: 2
rank: 0,1,2,2

BFS

Shortest Cycle in a Graph

private static final int MAX_LEN = 1000;

public int findShortestCycle(int n, int[][] edges) {
    List<Integer>[] graph = new List[n];
    for (int i = 0; i < n; i++) {
        graph[i] = new ArrayList<>();
    }

    for (int[] e : edges) {
        graph[e[0]].add(e[1]);
        graph[e[1]].add(e[0]);
    }

    int min = Integer.MAX_VALUE;
    for (int i = 0; i < n; i++) {
        min = Math.min(min, bfs(graph, i));
    }
    return min > n ? -1 : min;
}

private int bfs(List<Integer>[] graph, int node) {
    // distances[i]: distance from node to i
    int[] distances = new int[graph.length];
    Arrays.fill(distances, MAX_LEN);
    distances[node] = 0;

    Queue<Integer> q = new LinkedList<>();
    q.offer(node);
    int min = MAX_LEN;
    while (!q.isEmpty()) {
        node = q.poll();
        for (int child : graph[node]) {
            if (distances[child] == MAX_LEN) {
                distances[child] = distances[node] + 1;
                q.offer(child);
            } else if (distances[node] <= distances[child]) {
                // this condition ensures each node is processed only once
                min = Math.min(min, distances[node] + distances[child] + 1);
            }
        }
    }
    return min;
}