Graph
Representation
Nodes from 0 to n:
Map<Integer, List<Integer>>: unweightedMap<Integer, Map<Integer, Integer>>: weightedList<Integer>[]: unweightedList<int[]>[]: weighted
Coordinates:
Map<String, List<String>>:x + "#" + yMap<List<>, List<List<>>>:Arrays.asList(x, y)
Implicit:
Minimum Cost of a Path With Special Roads
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public int minimumCost(int[] start, int[] target, int[][] specialRoads) {
// considers only special roads that are cheaper than direct paths
List<int[]> roads = Arrays.stream(specialRoads)
.filter(r -> r[4] < getDistance(r[0], r[1], r[2], r[3]))
.collect(Collectors.toList());
// {road end, current min distance from src to the road end}
Map<List<Integer>, Integer> dist = new HashMap<>();
dist.put(Arrays.asList(start[0], start[1]), 0);
// {x, y, cost}
// the heap contains src and road ends
Queue<int[]> pq = new PriorityQueue<>((a, b) -> a[2] - b[2]);
pq.offer(new int[]{start[0], start[1], 0});
while (!pq.isEmpty()) {
int[] node = pq.poll();
for (int[] r : roads) {
// cost from current node to the road end
// = current cost + current node to the road start + road cost
int alt = node[2] + getDistance(node[0], node[1], r[0], r[1]) + r[4];
var k = Arrays.asList(r[2], r[3]);
if (alt < dist.getOrDefault(k, Integer.MAX_VALUE)) {
dist.put(k, alt);
pq.offer(new int[]{r[2], r[3], alt});
}
}
}
// completes the last mile - from road ends to the target
int min = getDistance(start[0], start[1], target[0], target[1]);
for (int[] r : roads) {
var k = Arrays.asList(r[2], r[3]);
if (dist.containsKey(k)) {
min = Math.min(min, dist.get(k) + getDistance(r[2], r[3], target[0], target[1]));
}
}
return min;
}
private int getDistance(int x1, int y1, int x2, int y2) {
return Math.abs(x1 - x2) + Math.abs(y1 - y2);
}
Connectivity
Bridge
Bridge: In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph’s number of connected components.
Equivalently, an edge is a bridge iff it is not contained in any cycle.
Tarjan’s bridge-finding algorithm
Linear time.
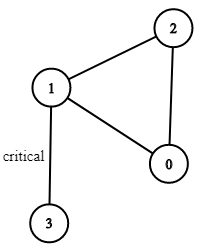
Critical Connections in a Network
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
private List<List<Integer>> graph;
private List<List<Integer>> bridges = new ArrayList<>();
private int time = 0;
// Tarjan's Algorithm
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
this.graph = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
for (List<Integer> e : connections) {
int s1 = e.get(0), s2 = e.get(1);
graph.get(s1).add(s2);
graph.get(s2).add(s1);
}
int[] dfn = new int[n]; // dfn[u]: the sequence number (timestamp) when node u is visited
int[] low = new int[n]; // low[u]: the timestamp of the earliest nodes in the stack to which the subtree of node u or node u can be traced (back edge)
dfs(dfn, low, 0, -1);
return bridges;
}
// preorder
private void dfs(int[] dfn, int[] low, int node, int parent) {
if (dfn[node] > 0) {
return;
}
dfn[node] = low[node] = ++time;
for (int neighbor : graph.get(node)) {
if (neighbor == parent) {
continue;
}
// unvisited
if (dfn[neighbor] == 0) {
dfs(dfn, low, neighbor, node);
}
low[node] = Math.min(low[node], low[neighbor]);
// no back edge; critical
if (low[neighbor] > dfn[node]) {
bridges.add(Arrays.asList(node, neighbor));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
node: 0
parent: -1
dfn: 1,0,0,0
low: 1,0,0,0
node: 1
parent: 0
dfn: 1,2,0,0
low: 1,2,0,0
node: 2
parent: 1
dfn: 1,2,3,0
low: 1,2,3,0
After DFS:
node: 2
parent: 1
dfn: 1,2,3,0
low: 1,2,1,0
node: 3
parent: 1
dfn: 1,2,3,4
low: 1,1,1,4
After DFS:
node: 3
parent: 1
dfn: 1,2,3,4
low: 1,1,1,4
After DFS:
node: 1
parent: 0
dfn: 1,2,3,4
low: 1,1,1,4
After DFS:
node: 0
parent: -1
dfn: 1,2,3,4
low: 1,1,1,4
Travelling Salesman Problem
Travelling salesman problem (TSP): “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?” It is an NP-hard problem.
Time complexity: \(O(n^22^n)\)
Maximum Cost of Trip With K Highways
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
private int[][] memo;
public int maximumCost(int n, int[][] highways, int k) {
if (k > n - 1) {
return -1;
}
List<int[]>[] graph = new List[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] h : highways) {
graph[h[0]].add(new int[]{h[1], h[2]});
graph[h[1]].add(new int[]{h[0], h[2]});
}
// memo[node][bitMask]
// no need to memoize k, because it can be inferred from the bit mask
this.memo = new int[n][(1 << n) - 1];
int max = -1;
for (int i = 0; i < n; i++) {
max = Math.max(max, dfs(graph, i, 1 << i, k));
}
return max < 0 ? -1 : max;
}
private int dfs(List<int[]>[] graph, int node, int mask, int k) {
if (k == 0) {
return 0;
}
if (memo[node][mask] == 0) {
memo[node][mask] = -1;
for (int[] e : graph[node]) {
int neighbor = e[0], toll = e[1];
if (((1 << neighbor) & mask) == 0) {
int next = dfs(graph, neighbor, mask | (1 << neighbor), k - 1);
if (next >= 0) {
memo[node][mask] = Math.max(memo[node][mask], toll + next);
}
}
}
}
return memo[node][mask];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public String shortestSuperstring(String[] words) {
int n = words.length;
// graph[i][j]: length of string to append when A[i] is followed by A[j]
int[][] graph = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
graph[i][j] = getDistance(words[i], words[j]);
graph[j][i] = getDistance(words[j], words[i]);
}
}
// Held–Karp algorithm
// dp[i][j]: min length
// path[i][j]: the node before j
// - i: bit mask, subset
// - j: last node travelled
int[][] dp = new int[1 << n][n], path = new int[1 << n][n];
int last = -1, min = Integer.MAX_VALUE;
// iterates all combinations/subsets of the nodes
for (int i = 1; i < (1 << n); i++) {
Arrays.fill(dp[i], Integer.MAX_VALUE);
// for each node
for (int j = 0; j < n; j++) {
// if the node (j) is in the subset
if ((i & (1 << j)) > 0) {
// the subset without the node (j)
int prev = i - (1 << j);
// if the node (j) is the only node in subset
if (prev == 0) {
dp[i][j] = words[j].length();
} else {
// for all the possible nodes before the node (j)
for (int k = 0; k < n; k++) {
// if k is valid and the length could be reduced
if (dp[prev][k] < Integer.MAX_VALUE && dp[prev][k] + graph[k][j] < dp[i][j]) {
dp[i][j] = dp[prev][k] + graph[k][j];
path[i][j] = k;
}
}
}
}
// subset contains all nodes
if (i == (1 << n) - 1 && dp[i][j] < min) {
min = dp[i][j];
last = j;
}
}
}
// restores the path
StringBuilder sb = new StringBuilder();
int set = (1 << n) - 1;
Deque<Integer> st = new ArrayDeque<>();
while (set > 0) {
st.push(last);
int tmp = set;
set -= (1 << last);
last = path[tmp][last];
}
// constructs the result
int i = st.pop();
sb.append(words[i]);
while (!st.isEmpty()) {
int j = st.pop();
sb.append(words[j].substring(words[j].length() - graph[i][j]));
i = j;
}
return sb.toString();
}
private int getDistance(String a, String b) {
// no string in words is a substirng of another string in words
for (int i = 1; i < a.length(); i++) {
if (b.startsWith(a.substring(i))) {
return b.length() - a.length() + i;
}
}
return b.length();
}
Directed Graph
Degree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findJudge(int n, vector<vector<int>>& trust) {
vector<int> degrees(n);
for (const auto& t : trust) {
degrees[t[0] - 1]--;
degrees[t[1] - 1]++;
}
for (int i = 0; i < n; i++) {
if (degrees[i] == n - 1) {
return i + 1;
}
}
return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int findCelebrity(int n) {
// finds the only candidate if it exists
int candidate = 0;
for (int i = 1; i < n; i++) {
if (knows(candidate, i)) {
candidate = i;
}
}
for (int i = 0; i < n; i++) {
// knows(candidate, i) is already checked in the first pass
if ((i < candidate && (knows(candidate, i) || !knows(i, candidate))) ||
(i > candidate && !knows(i, candidate))) {
return -1;
}
}
return candidate;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
private Map<String, Map<String, Double>> graph = new HashMap<>();
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
buildGraph(equations, values);
double[] result = new double[queries.size()];
for (int i = 0; i < queries.size(); i++) {
List<String> q = queries.get(i);
result[i] = getPathWeight(q.get(0), q.get(1), new HashSet<>());
}
return result;
}
private double getPathWeight(String start, String end, Set<String> visited) {
if (!graph.containsKey(start)) {
return -1.0;
}
if (graph.get(start).containsKey(end)) {
return graph.get(start).get(end);
}
// dfs
visited.add(start);
for (Map.Entry<String, Double> neighbour : graph.get(start).entrySet()) {
if (!visited.contains(neighbour.getKey())) {
double productWeight = getPathWeight(neighbour.getKey(), end, visited);
if (productWeight != -1.0) {
return neighbour.getValue() * productWeight;
}
}
}
return -1.0;
}
// A / B = k
// A : (B : k)
// B : (A : 1 / k)
private void buildGraph(List<List<String>> equations, double[] values) {
for (int i = 0; i < equations.size(); i++) {
List<String> e = equations.get(i);
graph.putIfAbsent(e.get(0), new HashMap<>());
graph.get(e.get(0)).put(e.get(1), values[i]);
graph.putIfAbsent(e.get(1), new HashMap<>());
graph.get(e.get(1)).put(e.get(0), 1 / values[i]);
}
}
Adjacency Matrix
Raising an adjacency matrix \(A\) of simple graph \(G\) to the \(n\)-th power gives the number of \(n\)-length walks between two vertices \(v_i\), \(v_j\) of \(G\) in the resulting matrix.
- A walk is a finite or infinite sequence of edges which joins a sequence of vertices.
- A trail is a walk in which all edges are distinct.
- A path is a trail in which all vertices (and therefore also all edges) are distinct.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
private static final int MOD = (int)1e9 + 7;
public int knightDialer(int n) {
if (n == 1) {
return 10;
}
// adjacent matrix
long[][] matrix = {
{0, 0, 0, 0, 1, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 1, 0, 0, 0, 1, 0},
{1, 0, 0, 1, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 1, 0, 0, 0, 0, 0},
};
long[][] pow = new long[10][10];
// identity matrix
for (int i = 0; i < pow.length; i++) {
pow[i][i] = 1;
}
// 50. Pow(x, n)
n--;
while (n > 0) {
if (n % 2 == 1) {
pow = multiply(pow, matrix);
}
matrix = multiply(matrix, matrix);
n /= 2;
}
long sum = 0;
for (int i = 0; i < pow.length; i++) {
for (int j = 0; j < pow[0].length; j++) {
sum = (sum + pow[i][j]) % MOD;
}
}
return (int)sum;
}
private long[][] multiply(long[][] m1, long[][] m2) {
int m = m1.length, l = m1[0].length, n = m2[0].length;
long[][] result = new long[10][10];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < l; k++) {
result[i][j] = (result[i][j] + m1[i][k] * m2[k][j]) % MOD;
}
}
}
return result;
}
Undirected Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
private List<Set<Integer>> graph = new ArrayList<>();
private Set<Integer> visited = new HashSet<>();
public boolean validTree(int n, int[][] edges) {
if (n != edges.length + 1) {
return false;
}
for (int i = 0; i < n; i++) {
graph.add(new HashSet<>());
}
for (int[] e : edges) {
graph.get(e[0]).add(e[1]);
graph.get(e[1]).add(e[0]);
}
// checks if the graph is fully connected
dfs(0);
return visited.size() == n;
}
private void dfs(int node) {
if (visited.contains(node)) {
return;
}
visited.add(node);
for (int neighbor : graph.get(node)) {
dfs(neighbor);
}
}
Another solution is by disjoint set.
Bipartite
Bipartite graph: a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V.
A graph is bipartite if and only if it does not contain an odd cycle.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public boolean isBipartite(int[][] graph) {
int n = graph.length;
// color[i] == 0: unvisited
// color[i] == 1 or -1: two valid colors
int[] colors = new int[n];
// checks all unvisited vertices since the graph might be disconnected
for (int i = 0; i < n; i++) {
if (colors[i] == 0 && !dfs(graph, colors, i, 1)) {
return false;
}
}
return true;
}
private boolean dfs(int[][] graph, int[] colors, int index, int expectedColor) {
// checks if the color of the node at the index is expected or not
if (colors[index] != 0) {
return colors[index] == expectedColor;
}
colors[index] = expectedColor;
for (int neighbor : graph[index]) {
if (!dfs(graph, colors, neighbor, -expectedColor)) {
return false;
}
}
return true;
}
Divide Nodes Into the Maximum Number of Groups
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public int magnificentSets(int n, int[][] edges) {
List<Integer>[] graph = new List[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] e : edges) {
graph[e[0]].add(e[1]);
graph[e[1]].add(e[0]);
}
// computes the shortest path between all pairs of nodes
int[][] dist = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
dist[i] = bfs(n, graph, i);
}
int[] colors = new int[n + 1];
// nodes in each component are connected
int[] components = new int[n + 1];
int componentId = 0, groups = 0;
for (int i = 1; i <= n; i++) {
if (colors[i] == 0) {
// the graph must be bipartite
// 785. Is Graph Bipartite?
if (!dfs(graph, colors, i, 1, components, ++componentId)) {
return -1;
}
// finds the max shortest path in the current component
int max = 0;
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
if (components[j] == componentId && components[k] == componentId) {
max = Math.max(max, dist[j][k]);
}
}
}
groups += max;
}
}
return groups;
}
private boolean dfs(List<Integer>[] graph, int[] colors, int index, int expectedColor, int[] components, int componentId) {
// checks if the color of the node at the index is expected or not
if (colors[index] != 0) {
return colors[index] == expectedColor;
}
colors[index] = expectedColor;
components[index] = componentId;
for (int neighbor : graph[index]) {
if (!dfs(graph, colors, neighbor, -expectedColor, components, componentId)) {
return false;
}
}
return true;
}
private int[] bfs(int n, List<Integer>[] graph, int src) {
// dist[i]: distance from src to vertex i
int[] dist = new int[n + 1];
Queue<Integer> q = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
int curr = src, d = 1;
dist[curr] = d++;
q.offer(curr);
visited.add(curr);
while (!q.isEmpty()) {
for (int i = q.size(); i > 0; i--) {
curr = q.poll();
for (int neighbor : graph[curr]) {
if (visited.add(neighbor)) {
q.offer(neighbor);
dist[neighbor] = d;
}
}
}
d++;
}
return dist;
}
Matching
Matching: a matching or independent edge set in an undirected graph is a set of edges without common vertices.
A maximum matching (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges.
Time complexity: \(O(\|V\|^3)\)
Hungarian algorithm: The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal–dual methods. The algorithm is known also as the Kuhn–Munkres algorithm or Munkres assignment algorithm.
Implementation: https://cp-algorithms.com/graph/kuhn_maximum_bipartite_matching.html
Maximum Number of Accepted Invitations
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
private int[][] grid;
private int m, n;
// Hungarian Algorithm
public int maximumInvitations(int[][] grid) {
this.grid = grid;
this.m = grid.length;
this.n = grid[0].length;
// matching[j]: the boy that invites the j-th girl
int[] matching = new int[n];
Arrays.fill(matching, -1);
int count = 0;
for (int i = 0; i < m; i++) {
if (dfs(i, matching, new boolean[n])) {
count++;
}
}
return count;
}
/**
* Checks if there's a matching for the given boy.
* @parameter i the index of the boy
* @parameter isAsked indicates whether each girl is already asked for invitation by any boy
* @return true if there's a girl that the boy invites, otherwise false
*/
private boolean dfs(int i, int[] matching, boolean[] isAsked) {
for (int j = 0; j < n; j++) {
// skips the girl if she cannot be invited
// or is already asked by the boy
if (grid[i][j] == 0 || isAsked[j]) {
continue;
}
// marks the girl as asked
isAsked[j] = true;
// if the girl is not yet invited
// or her boy can be matched to another girl
if (matching[j] == -1 || dfs(matching[j], matching, isAsked)) {
matching[j] = i;
return true;
}
}
return false;
}
Vertex Cover: vertex cover (sometimes node cover) of a graph is a set of vertices that includes at least one endpoint of every edge of the graph. It is NP-hard.
Kőnig’s theorem describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs.
Minimum Operations to Remove Adjacent Ones in Matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
private static final int[][] DIRECTIONS = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
private int[][] grid, match, visited;
private int m, n;
public int minimumOperations(int[][] grid) {
this.grid = grid;
this.m = grid.length;
this.n = grid[0].length;
// constructs a graph:
// if two 1-value cells are adjacent, then there's an edge between them
// we want to find the minimum vertex cover of this graph, so that
// removing all vertices in the set will make all the 1's disconneted
// minimum vertex cover <=> maximum matching
this.match = new int[m][n];
// visited[i][j]: the node (i, j) is visited in the attempt of visited[i][j]
this.visited = new int[m][n];
for (int i = 0; i < m; i++) {
Arrays.fill(match[i], -1);
Arrays.fill(visited[i], -1);
}
int count = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1 && match[i][j] < 0) {
if (dfs(i, j, visited[i][j] = i * n + j)) {
count++;
}
}
}
}
return count;
}
private boolean dfs(int i, int j, int v) {
for (int[] d : DIRECTIONS) {
int r = i + d[0], c = j + d[1];
if (r >= 0 && r < m && c >= 0 && c < n && grid[r][c] == 1 && visited[r][c] != v) {
visited[r][c] = v;
// augment path
if (match[r][c] < 0 || dfs(match[r][c] / n, match[r][c] % n, v)) {
match[r][c] = i * n + j;
match[i][j] = r * n + c;
return true;
}
}
}
return false;
}
Eulerian Path
Eulerian path: In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex.
Euler’s Theorem:
A connected graph has an Euler cycle if and only if every vertex has even degree.
A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component.
A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph.
Hierholzer’s Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private Map<String, Queue<String>> map = new HashMap<>();
private LinkedList<String> list = new LinkedList<>();
public List<String> findItinerary(List<List<String>> tickets) {
for (List<String> t : tickets) {
map.computeIfAbsent(t.get(0), k -> new PriorityQueue()).add(t.get(1));
}
visit("JFK");
return list;
}
private void visit(String node) {
while (map.containsKey(node) && !map.get(node).isEmpty()) {
// deletes visited vertex
visit(map.get(node).poll());
}
// postorder DFS
// current vertex is an exit
// adds the vertext to the route backwards
list.addFirst(node);
}
Dynamic Programming
The Most Similar Path in a Graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public List<Integer> mostSimilar(int n, int[][] roads, String[] names, String[] targetPath) {
List<Integer>[] graph = new ArrayList[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] r : roads) {
graph[r[0]].add(r[1]);
graph[r[1]].add(r[0]);
}
int m = targetPath.length;
// dp[i][j]: min edit distance for the path ending at node j compared to target path t[0] -> t[i]
int[][] dp = new int[m][n];
// initialization. max is bounded by the target path length m
for (int[] r : dp) {
Arrays.fill(r, m);
}
for (int j = 0; j < n; j++) {
dp[0][j] = names[j].equals(targetPath[0]) ? 0 : 1;
}
// stores the previous neighbor which has min edit distance
int[][] prev = new int[m][n];
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int neighbor : graph[j]) {
if (dp[i - 1][neighbor] < dp[i][j]) {
dp[i][j] = dp[i - 1][neighbor];
prev[i][j] = neighbor;
}
}
dp[i][j] += (names[j].equals(targetPath[i]) ? 0 : 1);
}
}
List<Integer> path = new ArrayList<>();
path.add(0);
// finds min dp[m - 1][j]
int min = m;
for (int j = 0; j < n; j++) {
if (dp[m - 1][j] < min) {
min = dp[m - 1][j];
path.set(0, j);
}
}
// restores the path
for (int i = m - 1; i > 0; i--) {
path.add(0, prev[i][path.get(0)]);
}
return path;
}