Fenwick Tree

Fenwick tree (Binary indexed tree)

A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

public class FenwickTree {
    private int[] nums;
    private int size;

    public FenwickTree(int size) {
        this.size = size;
        // one-based indexing is assumed
        nums = new int[size + 1];
    }

    /**
     * Returns the sum of the input elements with index from 1 to i (one-based indexing)
     * O(log(n))
     * @param i upper index of the range (one-based indexing)
     * @return sum of the input elements with index from 1 to i (one-based indexing)
     */
    public int sum(int i) {
        int sum = 0;
        while (i > 0)  {
            sum += nums[i];
            i -= lsb(i);
        }             
        return sum;
    }

    /**
     * Adds k to the input element with index i (one-based indexing)
     * O(log(n))
     * @param i index of the input element (one-based indexing)
     * @param k number to be added to the element
     */
    public void add(int i, int k) {
        while (i <= size) {
            nums[i] += k;
            i += lsb(i);
        }
    }

    private int lsb(int i) {
        return i & (-i);
    }
}

Range Sum Query - Mutable

Count of Smaller Numbers After Self

public List<Integer> countSmaller(int[] nums) {
    // deduplication
    // if i != j && nums[i] == nums[j]
    // i and j should occupy only one position in the Fenwick Tree
    Set<Integer> set = new TreeSet<>();
    for (int num : nums) {
        set.add(num);
    }

    int i = 0;
    Map<Integer, Integer> indices = new HashMap<>();
    for (int num : set) {
        indices.put(num, i++);
    }

    FenwickTree ft = new FenwickTree(indices.size());
    int n = nums.length;
    List<Integer> counts = new ArrayList<>(n);
    for (int j = n - 1; j >= 0; j--) {
        int index = indices.get(nums[j]);
        // `index` + 1 is the one-based index of nums[j]
        // so the index of max smaller number is `index`
        counts.add(0, ft.sum(index));
        ft.add(index + 1, 1);
    }
    return counts;
}

This problem can be solved by Merge Sort, too.

Similar problem:

Reverse Pairs

public int reversePairs(int[] nums) {
    // deduplication
    // if i != j && nums[i] == nums[j]
    // i and j should occupy only one position in the Fenwick Tree
    Set<Integer> set = new TreeSet<>();
    for (int num : nums) {
        set.add(num);
    }

    int i = 0;
    Map<Integer, Integer> indices = new HashMap<>();
    for (int num : set) {
        indices.put(num, i++);
    }

    FenwickTree ft = new FenwickTree(indices.size());
    int count = 0;
    List<Integer> list = new ArrayList<>(set);
    for (int j = nums.length - 1; j >= 0; j--) {
        // index of the pair of nums[j]
        int p = binarySearch(list, nums[j]);
        if (p >= 0) {
            count += ft.sum(indices.get(list.get(p)) + 1);
        }

        ft.add(indices.get(nums[j]) + 1, 1);
    }
    return count;
}

private int binarySearch(List<Integer> list, int target) {
    int low = 0, high = list.size() - 1;
    while (low < high) {
        int mid = (low + high + 1) >>> 1;
        if (2l * list.get(mid) < target) {
            low = mid;
        } else {
            high = mid - 1;
        }
    }
    return 2l * list.get(low) < target ? low : -1;
}

This problem can be solved by Merge Sort, too.

Count Number of Teams

private int MAX_RATING = (int)1e5;

public int numTeams(int[] rating) {
    FenwickTree left = new FenwickTree(MAX_RATING), right = new FenwickTree(MAX_RATING);

    // bucket counting
    // in the beginning, the middle soldier is at -1
    for (int r : rating) {
        right.add(r, 1);
    }

    int count = 0;
    for (int r : rating) {
        right.add(r, -1);
        count += left.sum(r - 1) * (right.sum(MAX_RATING) - right.sum(r));  // ascending
        count += (left.sum(MAX_RATING) - left.sum(r)) * right.sum(r - 1);  // descending
        left.add(r, 1);
    }

    return count;
}

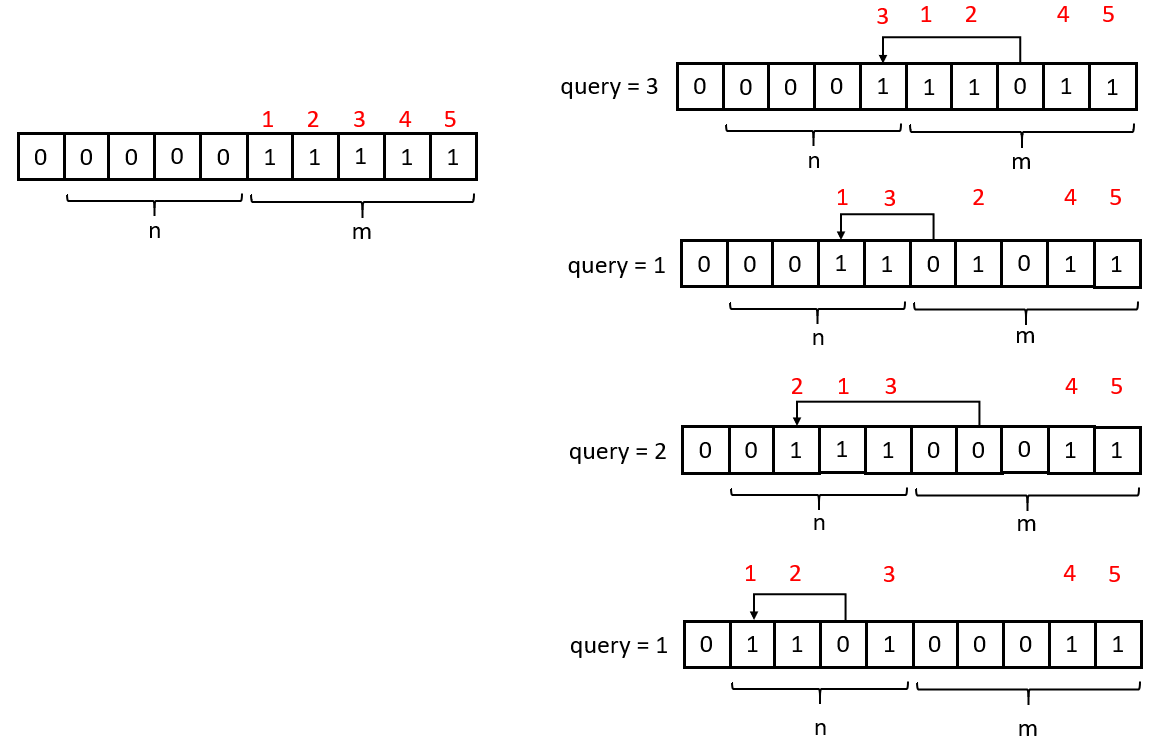
Queries on a Permutation With Key

public int[] processQueries(int[] queries, int m) {
    int n = queries.length;
    FenwickTree ft = new FenwickTree(n + m);
    int[] index = new int[m];

    // fills the last m positions with 1
    // [1...n] is default to 0
    for (int i = 1; i <= m; i++) {
        ft.add(n + i, 1);
        // memorizes index of the current element
        index[i - 1] = n + i;
    }

    int[] result = new int[n];
    for (int i = 0; i < queries.length; i++) {
        int curr = index[queries[i] - 1];
        result[i] = ft.sum(curr) - 1;

        // relocates queries[i] to a position in [1...n] in reverse order
        int next = n - i;
        ft.add(curr, -1);
        ft.add(next, 1);

        // updates the index of queries[i]
        index[queries[i] - 1] = next;
    }
    return result;
}

Create Sorted Array through Instructions

private static final int MOD = (int)1e9 + 7;

public int createSortedArray(int[] instructions) {
    FenwickTree ft = new FenwickTree(Arrays.stream(instructions).max().getAsInt());
    int cost = 0;
    for (int i = 0; i < instructions.length; i++) {
        cost = (int)(cost + Math.min(ft.sum(instructions[i] - 1), i - ft.sum(instructions[i])) % MOD) % MOD;
        ft.add(instructions[i], 1);
    }
    return cost;
}

Minimum Possible Integer After at Most K Adjacent Swaps On Digits

public String minInteger(String num, int k) {
    // index of each digit
    List<Queue<Integer>> list = new ArrayList<>(10);
    for (int i = 0; i <= 9; i++) {
        list.add(new LinkedList<>());
    }

    int n = num.length();
    for (int i = 0; i < n; i++) {
        list.get(num.charAt(i) - '0').offer(i);
    }

    StringBuilder sb = new StringBuilder();
    FenwickTree ft = new FenwickTree(n);

    for (int i = 0; i < n; i++) {
        // at current location, attempts to place 0...9
        for (int d = 0; d <= 9; d++) {
            if (list.get(d).size() != 0) {
                // finds the first occurrence of d
                int index = list.get(d).peek();
                // since a few numbers already shifted to left, this index might be outdated.
                // finds how many numbers got shifted to the left of index
                // e.g. "4192", k = 3
                // Round #1: d = 1, index = 1, shift = 0, "1492"
                // Round #2: d = 2, index = 3, shift = 1, "1249"
                int shift = ft.sum(index);
                // (index - shift) is number of swaps to make d move from index to i
                // ensures the d is in the k-size sliding window
                if (index - shift <= k) {
                    k -= index - shift;
                    // the "shift" value (calculated by ft.sum(num)) of all nums to the right of index
                    // would increase by 1
                    ft.add(index + 1, 1);
                    list.get(d).poll();
                    sb.append(d);
                    break;
                }
            }
        }
    }
    return sb.toString();
}

2D

Range Sum Query 2D - Mutable

private FenwickTree ft;
private int[][] nums;

public NumMatrix(int[][] matrix) {
    if (matrix.length == 0 || matrix[0].length == 0) {
        return;
    }

    int m = matrix.length, n = matrix[0].length;
    this.nums = new int[m][n];
    this.ft = new FenwickTree(m, n);

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            update(i, j, matrix[i][j]);
        }
    }
}

public void update(int row, int col, int val) {
    ft.add(row + 1, col + 1, val - nums[row][col]);
    nums[row][col] = val;
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    return ft.sum(row2 + 1, col2 + 1) - ft.sum(row1, col2 + 1) - ft.sum(row2 + 1, col1) + ft.sum(row1, col1);
}

public class FenwickTree {
    private int[][] grid;
    private int m, n;

    public FenwickTree(int m, int n) {
        this.m = m;
        this.n = n;
        // one-based indexing is assumed
        grid = new int[m + 1][n + 1];
    }

    // Returns the sum from index (1, 1) to (row, col)
    public int sum(int row, int col) {
        int sum = 0;
        for (int i = row; i > 0; i -= lsb(i)) {
            for (int j = col; j > 0; j -= lsb(j)) {
                sum += grid[i][j];
            }
        }          
        return sum;
    }

    // Adds k to element with index (row, col)
    public void add(int row, int col, int k) {
        for (int i = row; i <= m; i += lsb(i)) {
            for (int j = col; j <= n; j += lsb(j)) {
                grid[i][j] += k;
            }
        }
    }

    private int lsb(int i) {
        return i & (-i);
    }
}