Best Time to Buy and Sell Stock IV
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
// We can make maximum number of transactions
if (k >= n / 2) {
// 122. Best Time to Buy and Sell Stock II
int profit = 0;
for (int i = 1; i < n; i++) {
profit += max(0, prices[i] - prices[i - 1]);
}
return profit;
}
// dp[i][j]: max profit on j-th day with at most i transactions
vector<vector<int>> dp(k + 1, vector<int>(n));
for (int i = 1; i <= k; i++) {
for (int j = 1; j < n; j++) {
// Buy on day d
int mx = -prices[0];
for (int d = 1; d <= j; d++) {
mx = max(mx, dp[i - 1][d - 1] - prices[d]);
}
// Case 1: don't buy or sell
// Case 2: sell the stock
// prices[j] - prices[d]: profit of buying on day d and selling on day j
// max(dp[i - 1][d - 1] + prices[j] - prices[d])
// = prices[j] + max(dp[i - 1][d - 1] - prices[d])
dp[i][j] = max(dp[i][j - 1], prices[j] + mx);
}
}
return dp[k][n - 1];
}
|
Reduce the repetitive calculation of mx:
1
2
3
4
5
6
7
| for (int i = 1; i <= k; i++) {
int mx = -prices[0];
for (int j = 1; j < n; j++) {
mx = max(mx, dp[i - 1][j - 1] - prices[j]);
dp[i][j] = max(dp[i][j - 1], prices[j] + mx);
}
}
|
Swap the two for-loops and use an array to store the mx of each transaction:
1
2
3
4
5
6
7
| vector<int> mxs(k + 1, -prices[0]);
for (int i = 1; i < n; i++) {
for (int j = 1; j <= k; j++) {
mxs[j] = max(mxs[j], dp[j - 1][i - 1] - prices[i]);
dp[j][i] = max(dp[j][i - 1], prices[i] + mxs[j]);
}
}
|
Reduce to 1D:
1
2
3
4
5
6
7
8
| vector<int> dp(k + 1), mxs(k + 1, -prices[0]);
for (int i = 1; i < n; i++) {
for (int j = 1; j <= k; j++) {
mxs[j] = max(mxs[j], dp[j - 1] - prices[i]);
dp[j] = max(dp[j], prices[i] + mxs[j]);
}
}
return dp[k];
|
Best Time to Buy and Sell Stock III
In the last solution of Best Time to Buy and Sell Stock IV, replaces k with 2:
1
2
3
4
5
6
7
8
9
10
11
| public int maxProfit(int[] prices) {
int buy1 = Integer.MAX_VALUE, buy2 = Integer.MAX_VALUE;
int sell1 = 0, sell2 = 0;
for (int price : prices) {
buy1 = Math.min(buy1, price);
sell1 = Math.max(sell1, price - buy1);
buy2 = Math.min(buy2, price - sell1);
sell2 = Math.max(sell2, price - buy2);
}
return sell2;
}
|
Best Time to Buy and Sell Stock with Cooldown
1
| dp[i] = max(dp[i - 1], prices[i] - prices[j] + dp[j - 2]), j = [0, 1, ..., i - 1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int maxProfit(int[] prices) {
if (prices.length < 2) {
return 0;
}
int[] dp = new int[prices.length + 1];
int min = prices[0];
for (int i = 1; i < prices.length; i++) {
min = Math.min(min, prices[i] - dp[i - 1]);
dp[i + 1] = Math.max(dp[i], prices[i] - min);
}
return dp[prices.length];
}
|
Reduced to 0D:
1
2
3
4
5
6
7
8
| int prev = 0, curr = 0;
int min = prices[0];
for (int i = 1; i < prices.length; i++) {
min = Math.min(min, prices[i] - prev);
prev = curr;
curr = Math.max(curr, prices[i] - min);
}
return curr;
|
Number of Dice Rolls With Target Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int numRollsToTarget(int n, int k, int target) {
const int mod = 1e9 + 7;
vector<vector<int>> dp(n + 1, vector<int>(target + 1));
dp[n][0] = 1;
for (int i = n - 1; i >= 0; i--) {
for (int j = 1; j <= k; j++) {
for (int m = 0; m < target; m++) {
if (j + m <= target) {
dp[i][j + m] = (dp[i][j + m] + dp[i + 1][m]) % mod;
}
}
}
}
return dp[0][target];
}
|
Strange Printer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public int strangePrinter(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
for (int i = n - 1; i >= 0; i--) {
for (int len = 1; i + len < n; len++) {
int j = i + len;
if (s.charAt(i) == s.charAt(j)) {
// skips same characters
dp[i][j] = dp[i][j - 1];
} else {
// splits the string in many ways
dp[i][j] = Integer.MAX_VALUE;
for (int k = i; k + 1 <= j; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j]);
}
}
}
}
return dp[0][n - 1];
}
|
Cumulative Sum
Dice Roll Simulation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| private final int MOD = (int)1e9 + 7;
public int dieSimulator(int n, int[] rollMax) {
// dp[i][j]: number of distinct sequences at i-th roll and the last number is (j + 1)
// if j == 6, it's the total number of distinct sequences at i-th roll
int[][] dp = new int[n + 1][7];
// initialization
dp[0][6] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 6; j++) {
// if there's no constraint
dp[i][j] = dp[i - 1][6];
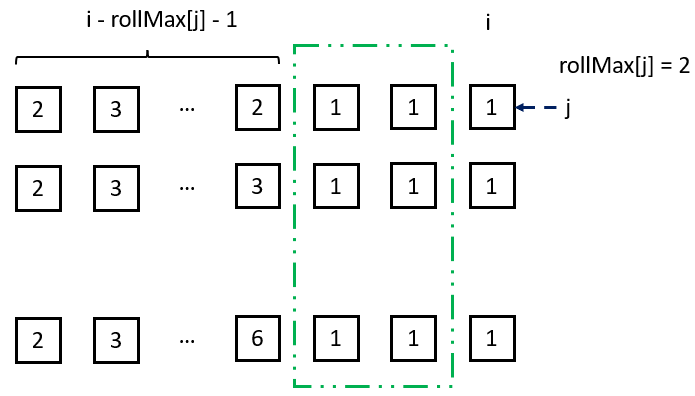
if (i - rollMax[j] > 0) {
// e.g. rollMax[j] = 2, and the rolls so far are: a, x, x, b
// if b == 1, then we should exclude all possible cases of a, 1, 1
// where a != 1
int reduction = dp[i - rollMax[j] - 1][6] - dp[i - rollMax[j] - 1][j];
dp[i][j] = ((dp[i][j] - reduction) % MOD + MOD) % MOD;
}
dp[i][6] = (dp[i][6] + dp[i][j]) % MOD;
}
}
return dp[n][6];
}
|
K Inverse Pairs Array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| int kInversePairs(int n, int k) {
const int mod = 1e9 + 7;
// Denote an array with n elements as a(n).
// Obviously, a(1) = 1.
// To construct a(n) from a(n -1), we append n to a(n - 1), then left shift n to its position.
// e.g. [2, 4, 1, 3] is constructed in the following steps:
// [1]
// [1, 2] -> [2, 1]
// [2, 1, 3]
// [2, 1, 3, 4] -> [2, 1, 4, 3] -> [2, 4, 1, 3]
//
// The total number of left shifts equals the number of inverse pairs in the final array.
// In the above example, there are 3 left shifts in total, so the number of inverse pairs is 3.
// dp[i][j]: the number of arrays of length i with exactly j inverse pairs.
vector<vector<int>> dp(n + 1, vector<int>(k + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
// There's only one dp[i][] array with no inverse pairs
dp[i][0] = 1;
for (int j = 1; j <= k; j++) {
// s is the number of left shifts of i.
// It represents the number of new inverse pairs introduced.
// s <= i - 1 because i - 1 is the number of elements in a(i - 1).
for (int s = 0; s <= min(j, i - 1); s++) {
dp[i][j] = (dp[i][j] + dp[i - 1][j - s]) % mod;
}
}
}
return dp[n][k];
}
|
The innermost loop can be removed by applying a recursive formula to the dynamic programming (DP) array, effectively optimizing the computation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int kInversePairs(int n, int k) {
vector<vector<int>> dp(n + 1, vector<int>(k + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
dp[i][0] = 1;
// dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] + ... + dp[i - 1][j - i + 1]
// => dp[i][j - 1] = dp[i - 1][j - 1] + dp[i - 1][j - 2] + ... + dp[i - 1][j - i]
// => dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - i]
for (int j = 1; j <= k; j++) {
dp[i][j] = (dp[i][j - 1] + dp[i - 1][j]) % mod;
if (j - i >= 0) {
dp[i][j] = (dp[i][j] - dp[i - 1][j - i] + mod) % mod;
}
}
}
return dp[n][k];
}
|
By implementing the rolling DP technique, we can further optimize our solution and significantly reduce memory consumption.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int kInversePairs(int n, int k) {
const int mod = 1e9 + 7;
vector<vector<int>> dp(2, vector<int>(k + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
dp[i % 2][0] = 1;
for (int j = 1; j <= k; j++) {
dp[i % 2][j] = (dp[i % 2][j - 1] + dp[(i - 1) % 2][j]) % mod;
if (j - i >= 0) {
dp[i % 2][j] = (dp[i % 2][j] - dp[(i - 1) % 2][j - i] + mod) % mod;
}
}
}
return dp[n % 2][k];
}
|