Combinatorics

Permutations

Permutations of multisets

\[{n \choose m_{1},m_{2},\ldots ,m_{l}}={\frac {n!}{m_{1}!\,m_{2}!\,\cdots \,m_{l}!}}=\frac {\left(\sum_{i=1}^{l}{m_{i}}\right)!}{\prod_{i=1}^{l}{m_{i}!}}\]

Probability of a Two Boxes Having The Same Number of Distinct Balls

private int n;
private long[] f;

public double getProbability(int[] balls) {
    int k = balls.length;

    this.n = Arrays.stream(balls).sum() / 2;

    this.f = new long[n + 1];
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        f[i] = f[i - 1] * i;
    }

    double[] good = new double[]{0}, all = new double[]{0};
    backtrack(balls, 0, new int[k], new int[k], good, all);

    return good[0] / all[0];
}

private void backtrack(int[] balls, int index, int[] box1, int[] box2, double[] good, double[] all) {
    if (index == balls.length) {
        // sum1 == sum2
        if (Arrays.stream(box1).sum() == n) {
            double p = (double)permutation(box1) * (double)permutation(box2);
            all[0] += p;

            long count1 = Arrays.stream(box1).filter(b -> b > 0).count();
            long count2 = Arrays.stream(box2).filter(b -> b > 0).count();
            good[0] += count1 == count2 ? p : 0;
        }
        return;
    }

    for (int i = 0; i <= balls[index]; i++) {
        box1[index] = i;
        box2[index] = balls[index] - i;
        backtrack(balls, index + 1, box1, box2, good, all);
        box1[index] = box2[index] = 0;
    }
}

private long permutation(int[] arr) {
    // permutations of multisets
    long prod = Arrays.stream(arr)
        .mapToLong(i -> f[i])
        .reduce(1, (a, b) -> a * b);
    return f[n] / prod;
}

De Bruijn Sequence

de Bruijn Sequence: de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring (i.e., as a contiguous subsequence)

The de Bruijn sequences can be constructed by taking a Hamiltonian path of an n-dimensional de Bruijn graph over k symbols (or equivalently, an Eulerian cycle of an (n − 1)-dimensional de Bruijn graph).

Cracking the Safe

public String crackSafe(int n, int k) {
    StringBuilder sb = new StringBuilder("0".repeat(n));

    Set<String> visited = new HashSet<>();
    visited.add(sb.toString());

    backtrack(sb, visited, (int)Math.pow(k, n), n, k);

    return sb.toString();
}

private boolean backtrack(StringBuilder sb, Set<String> visited, int target, int n, int k) {
    if (visited.size() == target) {
        return true;
    }

    // last (n - 1) digits
    String lastDigits = sb.substring(sb.length() - n + 1);
    for (char ch = '0'; ch < '0' + k; ch++) {
        String password = lastDigits + ch;
        if (visited.add(password))  {
            sb.append(ch);
            if (backtrack(sb, visited, target, n, k)) {
                return true;
            }
            visited.remove(password);
            sb.deleteCharAt(sb.length() - 1);
        }
    }

    return false;
}

Total Appeal of A String

public long appealSum(String s) {
    int[] last = new int[26];
    Arrays.fill(last, -1);

    int n = s.length();
    long count = 0;
    for (int i = 0; i < n; i++) {
        // the char at i appears in (i + 1) * (n - i)
        // also needs to subtract the duplicates: (last[ch] + 1) * (n - i)
        count += (i - last[s.charAt(i) - 'a']) * (n - i);
        last[s.charAt(i) - 'a'] = i;
    }
    return count;
}

Combinations

Count Sorted Vowel Strings

public int countVowelStrings(int n) {
    // comb(n + 4, 4)
    return (n + 4) * (n + 3) * (n + 2) * (n + 1) / 24;
}

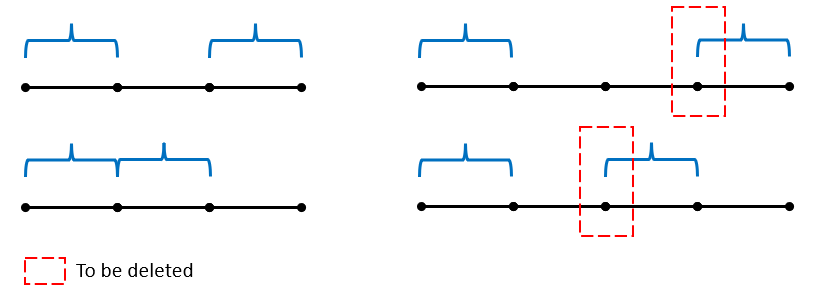
Number of Sets of K Non-Overlapping Line Segments

Equivalent to: n + k - 1 points, k segments, not allowed to share endpoints.

\[{\binom {n + k - 1}{2 * k}}\]

For example, n = 4, k = 2

Number of k-combinations

\[\binom {n}{k}=\prod _{i=1}^{k}{\frac {n+1-i}{i}}\]

\[{\binom {n}{k}}={\binom {n-1}{k-1}}+{\binom {n-1}{k}}\]

long[][] choose = new long[n][k];
for (int i = 0; i < choose.length; i++) {
    choose[i][0] = 1;
}

for (int i = 1; i < choose.length; i++) {
    for (int j = 1; j < choose[0].length; j++) {
        choose[i][j] = (choose[i - 1][j - 1] + choose[i - 1][j]) % mod;
    }
}

Kth Smallest Instructions

public String kthSmallestPath(int[] destination, int k) {
    int row = destination[0], col = destination[1];
    StringBuilder sb = new StringBuilder();
    int down = row;
    for (int i = 0; i < row + col; i++) {
        int count = choose[row + col - (i + 1)][down];

        // goes right
        if (count >= k) {
            sb.append("H");
        } else {
            // goes down
            down--;
            k -= count;
            sb.append("V");
        }
    }
    return sb.toString();
}

Indistinguishable Objects, Distinguishable Bins

Stars and Bars

Stars and bars

Theorem one

Positivity: Place \(n\) objects into \(k\) bins, such that all bins contain at least one object.

\[\binom {n-1}{k-1}\]

Count the Number of Ideal Arrays

private static final int MOD = (int)1e9 + 7;
// the max length of each array is 14, since 2 ^ 14 = 16384 > 10 ^ 4 (see comments for dp)
private static final int MAX_NUM_UNIQUE = 14;

public int idealArrays(int n, int maxValue) {
    // {element, divisors (not including the key itself)}
    Map<Integer, List<Integer>> map = new HashMap<>();
    for (int i = 1; i <= maxValue; i++) {
        for (int j = 2 * i; j <= maxValue; j += i) {
            map.computeIfAbsent(j, k -> new ArrayList<>()).add(i);
        }
    }

    // dp[i][j]: num of ideal arrays of length i ending with value j,
    // where each array doesn't contain duplicate numbers (strictly increasing)
    // this is a special case of the original problem, e.g. [1, 2, 4, 8], [3, 6, 12]
    // arr[i] % arr[i - 1] == 0
    long[][] dp = new long[MAX_NUM_UNIQUE + 1][maxValue + 1];
    Arrays.fill(dp[1], 1);

    // for the strictly increasing ideal arrays case
    for (int i = 2; i <= Math.min(n, MAX_NUM_UNIQUE); i++) {
        for (int j = 1; j <= maxValue; j++) {
            for (int k : map.getOrDefault(j, Collections.emptyList())) {
                dp[i][j] += dp[i - 1][k];
                dp[i][j] %= MOD;
            }
        }
    }

    // dp[i][0]: total number of strictly increasing ideal arrays of length i 
    dp[1][0] = 0;
    for (int i = 1; i <= Math.min(n, MAX_NUM_UNIQUE); i++) {
        for (int j = 1; j <= maxValue; j++) {
            dp[i][0] = (dp[i][0] + dp[i][j]) % MOD;
        }
    }

    // n choose k
    int[][] choose = new int[n + 1][MAX_NUM_UNIQUE + 1];
    for (int i = 0; i < choose.length; i++) {
        choose[i][0] = 1;
    }
    for (int i = 1; i < choose.length; i++) {
        for (int j = 1; j < choose[0].length; j++) {
            choose[i][j] = (choose[i - 1][j - 1] + choose[i - 1][j]) % MOD;
        }
    }

    // solves the original problem with starts and bars (Theorem one)
    int count = 0;
    for (int i = 1; i <= Math.min(n, MAX_NUM_UNIQUE); i++) {
        // e.g. [1, 2, 4], n = 5, len = 3
        // -> 1 1 | 2 | 4 4
        count += choose[n - 1][i - 1] * dp[i][0] % MOD;
        count %= MOD;
    }
    return count;
}

Theorem two

Number of combinations with repetition

Non-negativity: Place \(n\) objects into \(k\) bins. Some bins can be empty.

\[\left({\binom {k}{n}}\right)={\binom {n+k-1}{n}}\]

Distinguishable Objects, Indistinguishable Bins

Stirling numbers of the second kind: the number of ways to partition a set of n objects into k non-empty subsets.

\[S(n,k)={\frac {1}{k!}}\sum _{i=0}^{k}(-1)^{i}{\binom {k}{i}}(k-i)^{n}\]

Count Ways to Distribute Candies

private static final int MOD = (int)1e9 + 7;

public int waysToDistribute(int n, int k) {
    long[][] dp = new long[k + 1][n + 1];

    for (int i = 1; i <= k; i++) {
        dp[i][i] = 1;
        for (int j = i + 1; j <= n; j++) {
            dp[i][j] = (dp[i - 1][j - 1] + (dp[i][j - 1] * i) % MOD) % MOD;
        }
    }

    return (int)dp[k][n];
}